Do★Math 数学博物館 Mathematics Museum

今日5月23日を523と3ケタの数で表すと、523は素数です。西暦を含めた20170523は3187と6329の2つの素数で割り切れるので、素数ではありません。

皆さん、普通の視力検査では壁に検査表が貼ってあって、表の中の文字や記号が下に行くほど小さくなっていますよね。私たちがよく見る表では最下段は2.0となっていて、それ以上の視力を測ることはできません。実は、ほんとうの視力の決定方法（「定義」と言います）は次のように決まっています。
ランドルト環という大きさの決まった記号「Ｃ」を5メートル離れたところで見分けられると、視力は1.0です。そして、ランドルト環の大きさは変えずに、人が10メートルに離れたところで見分けることができると、視力は2.0です。そうです、視力と距離は比例しているのです。ランドルト環は眼科医エドムント・ランドルト (スイス　1846－1926) によって開発され、彼の名前がそのまま名称となりました。

本校3階数学教室前の廊下には西の壁に貼ってあるランドルト環からの距離を示してあります。5メートルおきに25メートルまで示してあるので、一度皆さんもチャレンジしてください。
（数学科 園田）

“Visual acuity testing”
We always see the chart for visual acuity on the wall. Characters or symbols get smaller as we look at the chart from top to bottom. In many cases, we can’t measure visual acuity of more than 2.0.
We will tell you about definition of visual acuity. If you can see “Ｃ”(a Landolt C) at a distance of 5 meters, your visual acuity is 1.0. If you can see it at the same size at 10 meters, your visual acuity is 2.0. You will see that visual acuity is in proportion to distance. A Landolt C is a symbol of an optotype that was developed by the Swiss-born ophthalmologist Edmund Landolt (1846－1926).
There is a Landolt C on the wall of the hallway on the 3rd floor. We indicate a distance from it, at 5, 10, 15, 20, and 25 meters on the floor.
Please come to Do★MATH and try!

今日5月9日を509と3ケタの数で表すと、509は素数です。西暦を含めた20170509は3で割り切れるので（3×6723503）、素数ではありません。

2¹、2²、2³から2³⁶までの数値をさまざまなもので表した展示です。最初のほうは、ビー玉や米粒をその個数分を実際に瓶に入れて展示していますが、値が大きくなるとイメージ写真で展示しています。米粒は一合（150ｇ）が約6500粒ということがインターネットで調べてわかりました。一部（2の20乗から30乗）を紹介します。

2の20乗 – 104万8576　　　エクセル画面の行数
2の21乗 – 209万7152　　　長野県の人口209万人
2の22乗 – 419万4304　　　宇宙最速の白色矮星「US 708」、420万km／時
2の23乗 – 838万8608　　　ブラジル国土851万km²
2の24乗 – 1677万7216　　 オランダ人口、約1700万人
2の25乗 – 3355万4432　　 錦織圭さんの年収３３５０万ドル(フォーブズ2016長者番付)
2の26乗 – 6710万8864　　 NASA深宇宙探査向けに高度ソーラー電気推進システム6700万ドル
2の27乗 – 1億3421万7728　世界で１年間に産まれる子ども約１億3000万人
2の28乗 – 2億6843万5456　世界の食肉生産量２.７億トン（豚・鶏・牛　FAO 2013）
2の29乗 – 5億3687万0912　カンブリア紀 5億5千万年前－5億年前
2の30乗 – 10億7374万1824 Lenovo 10億7000万色表示できるテレビ

この展示は、ドイツの数学博物館「Mathematikum」にあったものを参考に作りました。
（数学科　園田）

“2 to the nth power”
We have the exhibition of 2 to the nth power.
We made them by using marbles, grains of rice and photos.
For example, 6500 grains of rice weigh around 150 grams.
We will introduce some.

2^20 – 1,048,576　　the number of rows of Excel
2^21 – 2,097,152　　the population of Nagano prefecture
2^22 – 4,194,304　　the velocity of “US 708”, the Galaxy’s fastest-moving white dwarf star
2^23 – 8,388,608　　the area of Brazil
2^24 – 16,777,216　　the population of Netherlands
2^25 – 33,554,432　　Mr Nishikori Kei’s annual income (Forbes 2016)
2^26 – 67,108,864　　The Solar propulsion system for Space launch developed by NASA
2^27 – 134,217,728　 the number of children born every year in the world
2^28 – 268,435,456　 meat production in every year（pork・chicken・beef　FAO 2013）
2^29 – 536,870,912　 Cambrian period
2^30 – 1,073,741,824　the number of colour of TVs made by Lenovo Corporation

今日4月21日を421と3ケタの数で表すと、421は素数です。西暦を含めた20170421もなんと素数です！

２階ＭＳ（メディアスペース）に、円周率１万桁が記された雑誌のページを拡大したポスターを掲示しています。円周率が１万桁（けた）あれば、４桁で表される自分の誕生日や記念日か見つかる可能性が高いです。同志社の創立記念日11月29日（1129）、憲法記念日5月3日（0503）も見つかります。皆さんも自分の誕生日や家族の記念日を探してみてください。元ネタは「月刊円周率」（暗黒通信団発行）という雑誌です。雑誌の名前もおもしろいでしょう。
さらに、2階廊下（数学1教室と数学2教室の間）には、なんと円周率が5万桁書かれたポスターが展示されています。左上から、3.141592…と始まり、右下に5万桁目の数字1が書かれています。円周率は5万桁以降も無限に続く「無理数」と分類される数です。
このポスターはドイツ・フランクフルトの近く、ギーセンにある数学博物館で購入しました。この数学博物館Mathematikum（マスマティクム）を訪問したことが本校で博物館を作ろうと思い立ったきっかけです。（数学科 園田）

“The posters of pi”
We have a poster which shows 10000 digit of pi in our math museum on 2nd floor. Maybe you can find your birthday and memorial days written in 4 digit number in this poster. And you can find 29th November (1129) that is the day our school Doshisha was founded, 3rd May (0503) that is constitution day of Japan.
We have another poster of pi. 50000 digit of pi is written on the wall of the hallway. I went to German math museum “Mathematikum” at Guisen and bought it. I visited there and had an idea to make math museum in our school.

明日3月11日を311と3ケタの数で表すと、311は素数です。西暦を含めた20170311は、3と7、４３、そして3191で割ることができるので素数ではありません。（3/11は土曜日のため、今回は前日3/10に発信しました。）

今回は、夏の自由研究で、Rimse理数教育研究所主催「算数・数学の自由研究」作品全国コンクールで奨励賞を受賞された池田はるなさん（２年生）の作品を紹介します。
（主催者HP　http://www.rimse.or.jp/research/past/winner4th.html ）
テーマは「見た目の形と距離の関係 ～地面のタイルまでの距離が遠くなると，タイルが平たく見えるのはなぜだろう？？～」 です。
例えば、床の正方形のタイルを離れて見ていくと、形がだんだん平たくかつ台形に見えてきます。この現象を理解するには相似の関係とピタゴラスの定理、そして三角比の考え方が必要です。この原理を研究した池田さんのレポートはイラストや写真が多用されていて、たいへんわかりやすく仕上がっています。
池田さんは昨年の自由研究でも、「コップの容積をパッ！と求めるには!?」というテーマで、誰が読んでもわかりやすい表現で身の回りの疑問を中学生の数学を使って分析されていました。
彼女の作品は立志館2階数学MS1に展示してあります。
（数学科 園田）

“Relativity of the shape of appearance and distance”
This is the title of a student’s research during the last summer vacation part1.
We will introduce our student’s research work. Ikeda Haruna san (8th grade) got a prize in the competition by “Rimse” Research Institute of Mathematics and Science Education.
The title of research is“Relativity of the shape of appearance and distance – why is that the more the distance is until the tile on the ground, the more flat it seems become?”
When we see a square from a distance, it looks like a trapezoid. We need the theory of similarity, and Pythagorean theorem and a trigonometric ratio to understand this problem. She used many illustrations and photos, so we can understand her research content clearly.
Her research is exhibited on the second floor in our math space.

今日2月27日を227と3ケタの数で表すと、227は素数です。西暦を含めた20170227は、3×7×11×87317と素因数分解できるので素数ではありません。

今日2月27日を227と3ケタの数で表すと、227は素数です。西暦を含めた20170227は、3×7×11×87317と素因数分解できるので素数ではありません。
４つの４から四則演算で１つの数を作る遊びがあります。（英語では Four fours） 例えば、２を作るときは、４×４÷（４＋４）＝２ となります。 今回は、次の４つの数から１０を作ることにチャレンジしてください。
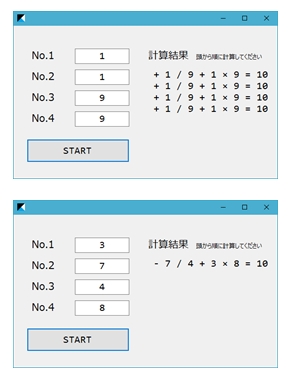（１）１、９、１、９を使って、１０を作ってください。
（２）３、４、７、８を使って、１０を作ってください。
答えを以下に示します。
（１）(１÷９＋１)×９＝１０
（２）(３－７÷４)×８＝１０
すでに何人かの生徒たちが正解を持ってきてくれています。この問題は、試行錯誤の中で答えが出てきます。また、今回の問題は答えがありますが、選ばれた4つの数からすべての数が計算できるわけではありません。まさに「数学」ですね。公式の暗記で素早く答えを出すのが数学ではありません。ゆっくりじっくり考えてみましょう。
今月の解答者の中に、この問題の答えを計算するプログラムを作ってきた人がいました。現在3年生の青木隆史さんです。私がこのブログで使っている素数判定プログラム「PrimeFactorization」を作ってくれたのも彼です。
今回の計算結果の画面とプログラムコードの一部を紹介しますね。
（数学科 園田）

“Finding the simplest mathematical expression by using four numbers from 1-9 and only common mathematical symbols”
We will talk about math quiz of February “Masu masu hatten koza” exhibited on the wall in Do★Math. Do you know the math puzzle “Four fours”? For example, “Make 2 by using four fours”, the solution is “4×4÷（4＋4）”. We asked our students,
（1）Make 10 by using 1, 9, 1, 9
（2）Make 10 by using 3, 4, 7, 8
The answers are the following.
（1）(1÷9＋1)×9＝10
（2）(3－7÷4)×8＝10
Some students answered to us. To solve the these problems, use trial and error and find answer. Please think hard and use trial and error.
One student made a program code to solve this problem. He is Mr. Aoki Takashi san (9th grade). He also made the program code “PrimeFactorization” to do the factorization in prime numbers that I usually use.
We will introduce the screenshots of the results of his calculations and the code he made in this blog.