Do★Math 数学博物館 Mathematics Museum

本日1月31日を131と3ケタの数で表すと、131は素数です。西暦を含めた20180131は23と877397という2つの素数で割り切れるので、素数ではありません。

前回のブログから、数学教室６室と教科ステーション（教員室）１室に付けている名前を紹介しています。今回は、数学2教室入口に掲示している「エラトステネス」のパネルと説明文をご紹介します。
説明文にあるように、エラトステネスはシエネとアレクサンドリアの緯度の差と距離から地球の大きさ（1周の長さ）を約46000kmと計算しました。これは、現在わかっている40000kmと15％程度の違いしかありませんでした。
（数学科　園田）

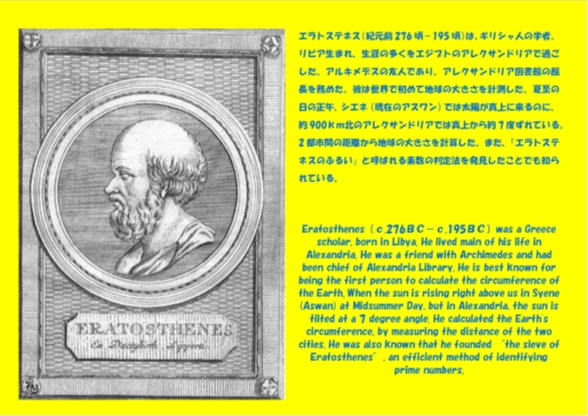
“The name of math classroom2 is ‘Eratostenes’.”
We introduced the name of the six math classrooms and the teacher’s “station” staff room from our last blog.
We will introduce the panel of “Eratostenes” and a document to explain the panel this time.
He calculated the circumference of the earth to be 46000 kilometers, by knowing the difference of latitude and the distance of the two cities, Cyene (Aswan) and Alexandria. The value is different from real one we know now within 15 percent.
by Tsuyoshi Sonoda (Math Dept.)

本日12月13日を1213と4ケタの数で表すと、1213は素数です。西暦を含めた20171213は2つの素数、109と185057の積で表されるので、素数ではありません。

以前、このブログでも紹介しましたが、本校は教科センター方式の学校運営を採用しており、教科専門教室があります。数学教室は全部で６教室あり、教科ステーションと呼ぶ教員室１部屋と合わせて 7室に数学者、科学者の名前をつけています。順に、数学1「ピタゴラス」、数学2「エラトステネス」、数学3「アインシュタイン」、数学4「伊能忠敬」、数学5「ガリレオ」、数学6「アルキメデス」、教科ステーションは「オイラー」です。今回は、数学1教室入口に掲示している「ピタゴラス」のパネルと説明文をご紹介します。
（数学科　園田）

“The name of math classroom 1 is ‘Pythagoras’.”
We introduced in this blog on July 19th, 2016 that we have six math classrooms in what we call “Subject Centered Style” in Japan.
We gave the names of famous mathematicians or scientists to the six classrooms and the teacher’s “station” staff room.
Math 1 is “Pythagoras”, math 2 is “Eratostenes”, math 3 is “Einstein”, math 4 is “Ino Tadataka”, math 5 is “Galileo”, math 6 is “Archimedes”, and “Euler” is for the staff room.
We will introduce the panel of “Pythagoras” and a document to explain the panel this time.
by Tsuyoshi Sonoda (Math Dept.)

今日11月9日を1109と4ケタの数で表すと、1109は素数です。西暦を含めた20171109は、3×7×751×1279と4つの素数に分解されるので、素数ではありません。

本校数学科は、平方根を楽しく学べる学習教材「ルートトランプ」を2014年春より製作、頒布を始めました。2017年11月現在、全国47都道府県で中学校を中心に2400個以上のご利用をいただいています。
Do★MATH2階メディアスペースには、カードを拡大したものを掲示しています。スートとともに書かれた4つの数はどれも同じ値「2」を示しています。

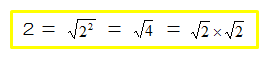
ルート1（√1）からルート75（√75）まで13種類のカードがありますから、普通のトランプで遊べるゲームは全てできます。ルート4（√4）= 2がありますから、「大富豪」だって楽しめるのです。
平方根をまだ学んでいない小学生の皆さんは、√の隣にある数を中に入れるときは2乗すること、√の中にある数どうしは普通にかけ算できること、この2つをルールとして覚えてください。中学生、お家の方と一緒に楽しめます。
（数学科 園田）

“Square Root Cards”
We made “Square Root Cards” to help study math with 9th grade students in 2014. Students can study square root happily using this card game.
Many schools in all the prefectures in Japan use more than 2400 sets at present.We show some big cards on the second floor in Do★MATH. The 4 cards mean the same value as follows.

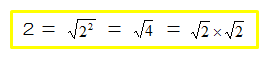
This card game consist of 13 kinds of cards, so we can play same the kinds of games as normal card games, such as Concentration, Old Maid, Sevens, Daifugo (Japanese card game) , and so on.
For elementary school students, you can also enjoy “Square Root Cards” with your family by knowing 2 rules, one is that we square the number when we put natural number into √ , the other is that we can multiply numbers in √ with each other.
Let’s enjoy it!
by Tsuyoshi Sonoda (Math Dept.)

今日10月31日を1031と4ケタの数で表すと、1031は素数です。西暦を含めた20171031は、3と37と181721という３つの素数で割り切れるので、素数ではありません。

ご存じの方も多いと思いますが、「マトリョーシカ人形」（ロシア語: Матрёшк、英語: Matryoshka doll）はロシアの民芸品です。
２分割の人形が3～5個重なったしくみになっており、外側の人形の上半身を外すと、小さい人形が次々に現れるようになっています。

それぞれの大きさの人形のサイズを測ってみると、だいたい相似の関係にありました。高さや円周の長さの比がほぼ同じだということです。

マトリョーシカという名称は、ロシアの女性名からきていて、スカーフ姿の若い女性の像が描かれているデザインがポピュラーですが、レーニンをはじめロシア・ソ連の歴代指導者が描かれたものや、動物など人間以外のものが描かれたものなど、絵柄は多様化してきています。本校では一般的なデザインの他、国立新美術館（東京）で購入したペンギンやマオリ族をデザインしたマトリョーシカ人形も3階ＭＳ（メディアスペース）に展示しています。また、日本にもマトリョーシカ人形と同じ作りでだるまなどの入れ子人形があります。
（数学科 園田）

“Matryoshka dolls are similar figures.”
Many Japanese people know that Matryoshka dolls are a folk craft made in Russia. The biggest doll includes 3 or 5 similar figures. When I measure the size, height and length of the circumference, of every doll, it is similar.
The name “Matryoshka”is named after a name of Russian lady, so the design of the scarf is popular with young ladies. Recently there are various designs, for example, leaders of Russia like Lenin and animals. We have a set of normal design’s, penguin’s and Maori people on the third floor in Do★MATH.
Please check it!
by Tsuyoshi Sonoda (Math Dept.)

今日10月21日を1021と4ケタの数で表すと、1021は素数です。西暦を含めた20171021は13で割り切れるので、素数ではありません。（10/21は土曜日のため、今回は10/23に発信しました。）

東京理科大学数学体験館の講座で「２進数ソーター」というツールを紹介され、本校でも作ってみました。これは、本ブログ2016年9月7日付で紹介した『誕生日当てゲーム』と原理は同じです。

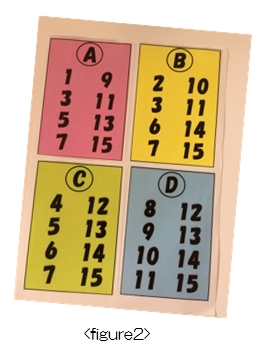
右下のＡ～Ｄのカードは、ある規則を持った数の集まりです。
まず、相手に１から１５までで好きな数を１つ思い浮かべてもらいます。次に、その数がＡからＤのカードに書いてあるかないかを順に聞いていきます。
原理を知っている人は、ここまでで相手の考えている数がわかります。今回は２進法ソーターがそれを当てます。
２進数ソーター（右写真）には１から15までの数が書かれた板が手前から奥に入っています。この遊び方を「10」の場合で紹介します。10はＢとＤのカードにあり、ＡとＣにはありません。
２進法ソーターの穴は右からＡからＤに対応しています。右から順に（Ｂ、Ｄの順）、10があるカードの記号の穴に棒を入れて板を持ち上げます。棒にひっかかったパネルを持ち上げ、手前に持ってきます。
これで10が1番前に出てきて、見事に当てることができました。
Do★MATHに展示していますので、ぜひチャレンジしてみてください。
（数学科 園田）

“Card sorter to guess the number”
Today, we will introduce about a game tool to guess the number using a binary system.
The game tool (figure1) consists of 15 panels with the numbers 1 to 15 written on them. There are 4 holes in each panel corresponding to “A” through ”D”. We can play the game by using this tool and 4 cards (figure2) that show different numbers each other.

First, the player chooses a number and the cards that show that number. For example, if the players chooses 10. the number is written on cards “B” and ”D”.
Then, we put a wooden pole into the holes in the panels and pull them up and put those panels in the front. Lastly, the panel that shows the number 10 will be in the front.

This game tool applies the binary number system used by computers. We introduced other game in our blog on September 7th, 2016. It has a same principle with this card sorter.
We exhibits it in Do★MATH.
Let’s try it together!
by Tsuyoshi Sonoda (Math Dept.)