Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース（「数学メディアスペース」）を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。
※こちらのイベントは終了しました。
★3種類まとめて購入すると、送料無料！（2020年9月より当面の間）
「アテナイの学堂」 － 数学者、科学者と哲学者の出会い －
本日5月3日を503と3ケタの数で表すと、503は素数です。西暦を含めた20180503は72×37×11131と素因数分解できるので、素数ではありません。（5月3日は休日のため、今回は5月2日に発信しました。）
「アテナイの学堂」は、ルネサンス期の画家ラファエロ（1483-1520）の傑作の一つと言われています。ローマにあるバチカン宮殿にはラファエロの間と呼ばれる4つの部屋があります。「アテナイの学堂」はその中の1部屋「署名の間」の壁に描かれたタテ5m、ヨコ7mの大きなフレスコ画です。この作品は、ギリシャ文明期の建物の中に集まる数学者、哲学者を描いた想像画で、当時より1500年前の時代を想像して描かれました。
今回は、この絵の中に出てくる数学者、科学者と哲学者を紹介しましょう。
まず、中央には、この絵の主役とも言える2人の哲学者、プラトン（左 モデルはレオナルド・ダ・ビンチとされています）とアリストテレス（右）が描かれています。プラトンの数人左に哲学者のソクラテスがいます。
階段下右方で、コンパスを持ち、弟子に説明している人物が数学者ユークリッド（紀元前3世紀頃）です。ユークリッド幾何学をまとめた書物「原論」で有名です。
その隣の、地球儀を持った後ろ向きの人物が天動説で有名な天文学者、数学者のプトレマイオス（ 2世紀頃）です。「天動説」を英語で「Ptolemaic theory」と表すのは彼の名前から来ています。そして、彼の右に作者のラファエロがいます。（前を向き、肩と顔が見えている人です。）
世界で最も有名な定理の一つを発見したとされる数学者ピタゴラス（紀元前570頃－紀元前495頃）は、画面左下で、ひざまづいて書物を調べている人です。
さらに、ピタゴラスの右上に描かれている女性は、アエギュプトゥス(現在のエジプト)の数学者、天文学者のヒュパティア（350～370頃－415）です。彼女は、天体観測儀（アストロラーベ）と液体比重計（ハイドロスコープ）を完成したと伝えられています。
今回のブログでは、4人の数学者と3人の哲学者を紹介しました。「アテナイの学堂」を見る機会があれば、ぜひ学者たちを探してみてください。「アテナイの学堂」はメディアスペース3階に展示してあります。
（数学科 園田）
“School of Athens’ － An encounter with mathematicians, scientists and philosophers －”
“School of Athens” is a masterpiece of Raphael’s works. Raphael (1483-1520) was an artist in the renaissance period. “School of Athens” is located in the “Room of the Segnatura”, one of the four Raphael Rooms in the Apostolic Palace in the Vatican. It measures 5 meters high by 7 meters wide and was drawn in fresco.
We will introduce some mathematicians, scientists and philosophers.
There are Plato (left) and Aristotle (right) in the center of the picture.
Socrates is a few people left of Plato.
Mathematician Euclid (3rd century BC) is the one who is explaining to his pupils with compass in the lower left of downstairs. He is well known for Euclid’s Elements.
Ptolemy (c. AD 100－c. 170), who is well known for Ptolemaic theory, is an Astronomer and Mathematician who has globe next to Euclid in the picture. And Raphael is right of Ptolemy.
Mathematician Pythagoras (c.570BC－c.495BC), who found the most famous theory, is the one who is researching the book on his knees in the lower left in the picture.
Finally, a woman on the upper right of Pythagoras is Egyptian mathematician and astronomer Hypatia (c.350 – 370－415). She has constructed astrolabes and hydrometers.
We talk about four mathematicians and three philosophers in this blog. Let’s find them when you see “School of Athens”. “School of Athens” is exhibited on the third floor in our math space.
by Tsuyoshi Sonoda (Math Dept.)
出典 http://www.kabegamilink.com/act/0706/03530.html
数学教室5「ガリレオ・ガリレイ」
本日4月21日を421と3ケタの数で表すと、421は素数です。西暦を含めた20180421は35×83047と素因数分解できるので、素数ではありません。（4月21日は休日のため、今回は4月20日に発信しました。）
今回は、数学5教室入口に掲示している「ガリレオ・ガリレイ」のパネルと説明文をご紹介します。
日本語では違和感がありますが、私たちが通常使う「ガリレオ」は名前です。「ガリレイ」が姓です。ちなみにミケランジェロ、ダンテ、ナポレオンも名前です。
それ以前は「間違っている」、「異端だ」と言われた地動説（紀元前3世紀、アリスタルコスというギリシャの天文学者、数学者が天動説を主張しています）は、コペルニクス（1473-1543）やガリレオ（1564-1642）、そしてニュートン（1643-1727）によって、市民の常識となりました。
ガリレオは、1609年に独自の望遠鏡を作り、月や木星を観測しました。月にクレーターを発見して、月が完全な球体でないことを見つけ、さらに1610年、木星に4つの惑星を発見しました。天動説は、地球が中心だから月はその周りをまわっているという説明をしていたので、木星が衛星を持っているという発見は天動説には不利な事実でした。
（数学科 園田）
1609年には自作の望遠鏡で月のクレーターや木星の４つの衛星を観測した。著作「天文対話」で地動説を主張して、宗教裁判にかけられた。
Galileo Galilei（1564－1642）was an Italian physicist and astronomer. He taught geometry, mathematics and astronomy. He found that the distance of objects falling was directly proportional to square of the falling time. He rolled two spheres that were different weights but the same shape, and demonstrated that their velocity was the same. His discovery of the law of falling led to the law of universal gravitation. He also observed the moon and 4 Jovian planets by a telescope of his own making in 1609. He argued the heliocentric systems in his book “Dialogue Concerning the Two Chief World Systems”, but he lost the case.
“The name of math classroom 5 is ‘Galileo Galilei ’.”
We will introduce the panel of “Galileo Galilei” and a document to explain the panel this time.
It may feel strange that ‘Galileo’ is a first name, and ‘Galilei is a family name. For example, Michelangelo, Dante, and Napoleon are the same.
Copernican theory, which had been regarded as wrong and unorthodox, became common sense by contributions from Copernicus (1472－1543), Galileo (1564－1642) and Newton (1643－1727).
Galileo made a telescope and observed the moon and Jupiter. He discovered craters on the moon and 4 Jovian planets. Ptolemaic theory explained that the earth is the center of the universe, so the moon moves around the earth. So the discovery of the Jovian planets had a disadvantage for Ptolemaic theory.
by Tsuyoshi Sonoda (Math Dept.)
おむすびころりん徹底検証！！ ～2017自由研究作品1～
本日3月7日を307と3ケタの数で表すと、307は素数です。西暦を含めた20180307は3×7×7×107×1283と素因数分解できるので、素数ではありません。（次回は4月中旬に発信します。）
今回は、夏の自由研究で、昨年に引き続き、Rimse理数教育研究所主催「算数・数学の自由研究」作品全国コンクールで敢闘賞を受賞された池田はるなさん（3年生）の作品を紹介します。
（主催者HP http://www.rimse.or.jp/research/past/winner5th.html ）
テーマは「おじいさんはおむすびに追いつけたのか！？ おむすびころりん徹底検証！！」 です。
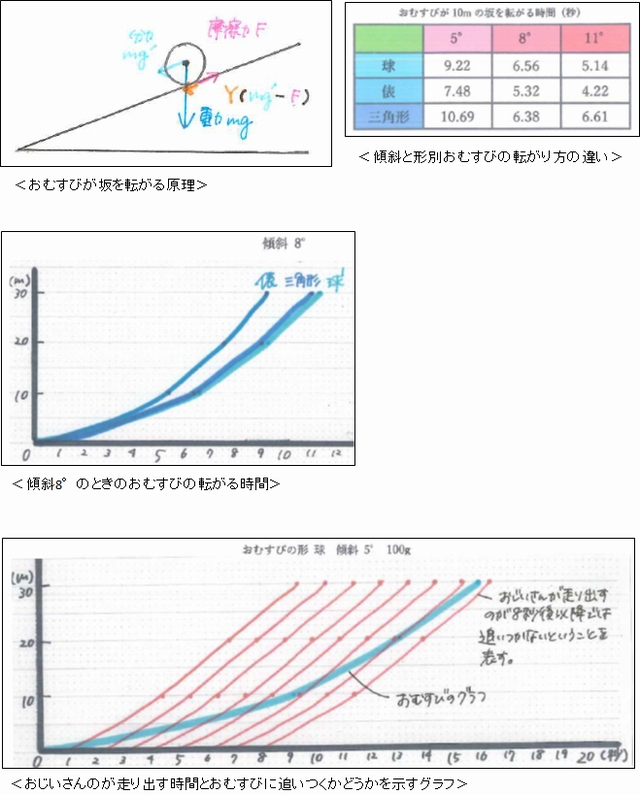
日本のおとぎ話として有名な「おむすびころりん」では、おじいさんはおばあさんが作ってくれたおむすびを落としてしまい、おむすびは山の斜面を転がります。おじいさんはすぐ追いかけましたが追いつけずに、おむすびは木の根元にあった穴に落ちてしまったという設定でお話は展開していきます。池田さんのレポートは、高校の物理で学ぶ運動法則ｘ＝ｖ0ｔ＋
ａｔ2（ｘ：移動距離、ｖ0：初速度、ｔ：時間、ａ：加速度）を使って、このお話を実際に実験、検証しています。傾斜の角度、おむすびの形・重さ、おじいさんの走る速さを変えて実験し、それぞれの影響を分析しました。イラストや実験データ・グラフが多用されていて、読ませるレポートに仕上がっています。
彼女は1年次に「コップの容積をパッ！と求めるには!?」というテーマで、2年次には「見た目の形と距離の関係 ～地面のタイルまでの距離が遠くなると，タイルが平たく見えるのはなぜだろう？？～」というテーマで数学の自由研究にとりくみました。どれもたいへんわかりやすいレポートです。
池田はるなさんの作品はすべて立志館2階数学MS1に展示してあります。
（数学科 園田）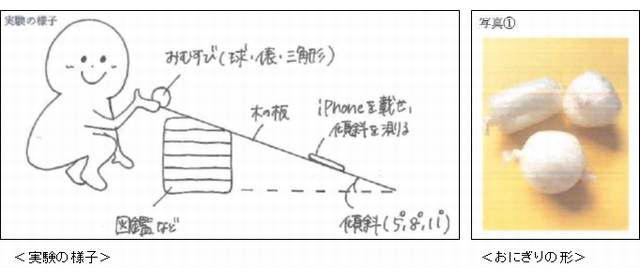
“Thorough Research of ’Omusubi Kororin’”
This is the title of a student’s research during the last summer vacation part1.
We will introduce our student’s research work. Ikeda Haruna san (9th grade) got a prize in the competition by “Rimse” Research Institute of Mathematics and Science Education for two years in a row.
The title of her research is “Thorough Research of ’Omusubi Kororin’ – did an old man catch up with an Omusubi?”
In an old Japanese story called ‘Omusubi kororin’, an old man dropped an omusubi that an old woman made for him and it was rolling down the slope of the mountain. He ran and tried to catch up with the omusubi, but he could not and it fell in a hole near the foot of a tree and the story continued. Ikeda san used the law of motion ‘ｘ＝ｖ0ｔ＋ａｔ2（ｘ : movement distance, ｖ0 : initial velocity, ｔ : time, ａ : accelration）’ and researched this story. She changed conditions of the degree of the slope, the shape and weight of the omusubi and the velocity of the old man running and tested it. And she verified the influence of those conditions. Her report used many illustrations and graphs, it was a very rewarding work.
She made projects, ‘How to get the cubic contents of glasses’ in the 7th grade and ‘Relativity of the shape of appearance and distance – why is that the more further away the tile on the ground is, the more flat it seems to become?’ in the 8th grade. Both research contents were very clear.
All of her research projects are exhibited on the second floor in our math space.
by Tsuyoshi Sonoda (Math Dept.)
Click Here for report(PDF)
数学教室4「伊能忠敬」
本日2月27日を227と3ケタの数で表すと、227は素数です。西暦を含めた20180227は53、349、1091という3つの素数で割り切れるので、素数ではありません。
今回は、立志館3階、数学4教室入口に掲示している「伊能忠敬」のパネルと説明文をご紹介します。
伊能忠敬は55才から71才まで10回の測量を行い、大図214枚、中図8枚、小図3枚の「大日本沿海與地全図」を完成させました。大図の縮尺は36000分の1です。彼が測量できなかった北海道北西部は、樺太を探検し間宮海峡を発見した間宮林蔵が測量し、地図が作られました。
伊能忠敬の功績を記念して、彼が家業を営んだ千葉県香取市に伊能忠敬記念館があります。彼の作った地図を直接見ることができます。ぜひ一度ご覧になってください。
（数学科 園田）
Ino Tadataka （1745－1818) was a Japanese surveyor. He is known for completing the first map of Japan created using modern surveying techniques. He went to Edo (Tokyo) and became a pupil of astronomer Takahashi Koretoki, at the age of 50. He went to survey Ezo land(Hokkaido) in 1800. He travelled all the country except for a region in northwestern Hokkaido for 17 years. After 3 years later, his pupils completed“Dai Nihon Enkai Yoti Zenzu”. The original ware lost by fire in 1873, but all copies (214 pieces) were found in 2001 and later. As to the length of a degree of the meridian, he calculated it was 28.2-ri (110.75km), a quite accurate figure compared even with today’s measurements.
“The name of math classroom 4 is ‘Ino Tadataka’.”
We will introduce the panel of “Ino Tadataka” and a document to explain the panel this time.
Ino Tadataka surveyed all the country 10 times from when he was 55 to 71 years old, and he made “Dai Nihon Enkai Yoti Zenzu” with “Dai-zu” of 214 pieces, “Chu-zu” of 8 pieces and “Sho-zu” of 3 pieces. “Dai-zu” are maps drawn on a scale of 1 to 36000. Mamiya Rinzo who explored Karafuto (Sakhalin) and discovered the Mamiya Strait (the Tatar Strait) surveyed northwestern Hokkaido where Ino Tadataka could not survey.
There is an Ino Tadataka museum at Katori-city, Chiba-prefecture. There we can directly see the maps he made. I recommend that you go there.
by Tsuyoshi Sonoda (Math Dept.)
数学教室3「アインシュタイン」
本日2月11日を211と3ケタの数で表すと、211は素数です。西暦を含めた20180211は2つの素数、3と6726737の積で表されるので、素数ではありません。（2月11日は休日のため、今回は2月9日に発信しました。）
前々回のブログから、数学教室６室と教科ステーション（教員室）に付けている名前を紹介しています。今回は、数学3教室入口に掲示している「アインシュタイン」のパネルとその説明文をご紹介します。
皆さんが電車に乗ったとき、すれ違う電車を見ると、その電車は自分の乗っている電車の速さが足されて倍の速さで動いているように感じた経験があると思います。また、隣どうしでホームに止まっている電車が動き始めたとき、自分の乗っている電車が動き始めたように感じたことはありませんか。このように、速さというのは相対的なものです。
しかし、光の速さだけはどのような条件で測っても秒速30万kmになります。アインシュタインはこの不思議な現象に疑問を持ち、研究を続けて相対性理論を完成しました。とても不思議に感じますが、相対性理論は状況の違いで時間の進み方が変わることを説明しています。
このことは、実際に私たちのまわりで活用されています。例えば、ＧＰＳ機能（衛星測位システム）に利用されている人工衛星では、地球上より時間が速く進むので、時間を調整しないと1日に10km以上位置がずれてしまいます。そのため、人工衛星側の時計は1日に100万分の38秒だけ遅く進むように補正されています。
（数学科 園田）
（イメージ写真は「ＲＩＣＯＨサイエンス資料館」より転載
http://jp.ricoh.com/kouken/science_caravan/science/gst008.html）
Albert Einstein（1879－1955）was a Jewish scientist, born in Germany. He proposed “the special theory of relativity”in 1905. He presented “general theory of relativity”and won the Nobel prize for physics in 1922. He visited to Japan and stayed for a month in the autumn of 1922. There are great results than the above. For example, quantum theory of light and a Brownian motion. In 1933, he immigrated to US to avoid persecution of Nazi and lived in Princeton. He requested to president to make atomic bomb. But his old days, he was against the war with many scientist.
“The name of math classroom 3 is ‘Einstein’.”
We introduced the name of the six math classrooms and the teacher’s “station” staff room from our before last blog.
We will introduce the panel of “Einstein” and a document to explain the panel this time.
We maybe have an experience where we see train across the tracks run at twice the speed of our train. We also feel our train started to move when a train across the tracks did. Speed is relative like this. But only speed of light is constant. Einstein had a doubt about this fact and promoted research, and finally he completed “Theory of relativity”. You may feel it is a curious thing. “Theory of relativity” explains that the way of time proceeds different in different situations. For example, time on a GPS satellite is faster than on the earth, so it is more than 10 kilometers off the exact position a day without time correction. So a clock on a GPS satellite is corrected to be late by 38 seconds of 1 million per day.
by Tsuyoshi Sonoda (Math Dept.)
