Do★Math 数学博物館 Mathematics Museum

今日2月23日を223と3ケタの数で表すと、223は素数です。なんと西暦を含めた20170223も素数です。しかし、2月は素数で表せる日の少ない月です。2/11、 2/23 、2/27、 2/29、うるう年でも４日しかありません。

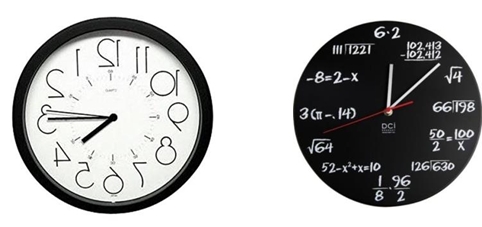
数学ゾーンの4箇所の入り口には、変わった時計が掛けてあります。
1種類（日本製）は鏡文字で数字が書かれています。2階数学ゾーン入口に掛けてあります。廊下の反対側に鏡を置いているので、鏡越しに時計を見てください。
もう1種類（アメリカ製）はいろいろな表記で1から12が刻まれています。1時は「102413－10241」、2時は「」、3時は「」というふうに表示されています。（数学科　園田）

“The curious clocks”
There are strange clocks on the wall at the entrance of Do MATH.
One clock (made in Japan) in the east on the second floor has numbers written in mirror writing. We placed a mirror at the opposite side of the hallway, so we can see the real characters in the clock through the mirror.
The other is made in USA. The numbers are described in various ways. For example, 1 is “102413－102412”, 2 is “”, 3 is “”.

皆さま、明けましておめでとうございます。本年もどうぞよろしくお願いいたします。
今日1月27日を127と3ケタの数で表すと、127は素数です。西暦を含めた20170127は、151×223×599と素因数分解できるので素数ではありません。

4種類8つのパーツを一つの立方体に組み立てて遊びます。
この操作は、x³+3x²y+3xy²+y³ … (1) という式（「展開」された状態）が、(x+y)³ … (2) という式（「因数分解」された状態）同じであることを意味しています。(1)の式とパーツの関係を見ていきましょう。(1)の式のx³は１辺の長さがｘの立方体の体積、3x²yが各辺ｘ、ｘ、ｙの直方体３個分の体積、3xy²が各辺ｘ、ｙ、ｙの直方体３個分の体積、y³が１辺ｙの立方体の体積を表しているのです。
もうおわかりですね。最初、ばらばらに置かれた状態が展開の式（1）です。組み立てられて１辺の長さx+yの立方体になった状態が因数分解の式（2）です。
数学博物館には、2次式の因数分解を説明する平板の「展開・因数分解パズル」もあります。
ぜひ体験しにいらっしゃってください。（数学科 園田）

“The cube puzzle”
We play this cube puzzle by gathering 8 parts composed of 4 kinds of blocks. This activity means that x³+3x²y+3xy²+y³…(1) is the same value as (x+y)³…(2). We can see that “x³” is the volume of a cube with sides x, “3x²y” is the volume of 3 rectangular solids with each side ｘ, ｘ and ｙ, “3xy²” is the volume of 3 rectangular solids with each sides of ｘ and ｙ and y, “y³” is the volume of a cube with sides ｙ.
So you can see that expression (1) means expansion and expression (2) means factorization by making a big cube with side (x+y).
We have another puzzle that explains expression and factorization in Do★MATH.
Let’s try it together!

本日12月13日を1213と4ケタの数で表すと、1213は素数です。西暦を含めた20161213は、73×276181と素因数分解できるので素数ではありません。

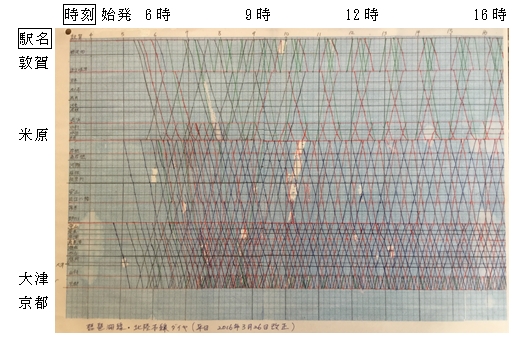
今回は、2016年度3年生の中嶋菊之くんが自由研究で作成したＪＲ北陸本線と琵琶湖線（東海道本線）、敦賀（つるが）から京都までのダイヤグラムを紹介します。ダイヤグラムとは、時刻表をグラフで表したものです。
縦軸は距離（駅名）、横軸は時間です。普通、快速、新快速、特急の４種別の列車を、それぞれ黒、青、赤、緑と区別しています。始発から終電までの全旅客列車のスケジュールが入っていて、駅での停車時間もわかります。昔は、ダイヤグラム専門の職人（「スジ屋」と呼ばれているそうです。映画「交渉人 真下正義」では「線引き屋」という名前で登場していました。）が鉛筆とものさしを使い、知識と経験を駆使して書いていました。中嶋くんも「スジひき」と表現しています。今、ダイヤグラムはコンピュータを使って作成されています。
2年生で学習する「一次関数」の知識があれば、より深く楽しめます。

＜中嶋くんの作成したダイヤグラム＞
誌面の関係で、半分（始発から16時台まで）を紹介します。

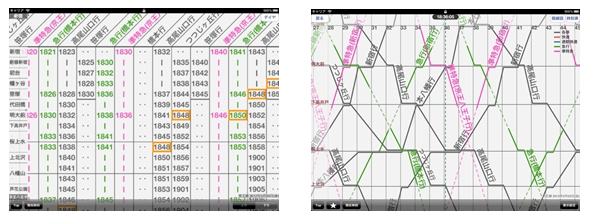
＜参考＞
京王線「新宿－八王子」間の時刻表（左）とダイヤグラム（右）

“Diagram”
This graph is a “Diagram”, which shows the time table of the JR Hokuriku line and Biwako line (Tokaido line) from Tsuruga station to Kyoto station, made by Nakajima Kikuyuki san. He is in the 9th grade in 2016.
The vertical axis shows the distance between stations. And the horizontal axis shows the time. Local trains are indicated by black lines, rapid trains are blue, special rapid trains are red and limited expresses are green. It shows all the passenger trains for a day. You can also see how long trains will stop at the station.
In the past, there were professional craftsmen, who wrote it using pencils and straight edges. He also wrote it by pen. But now it is written by computers.
If you have studied “Linear function”, you will be able to enjoy this diagram much more.

明日11月29日を1129と4ケタの数で表すと、1129は素数です。本校の創立記念日は11月29日、1129は素数でした！ちなみに、西暦を含めた20161129は、31×650359と素因数分解できるので素数ではありません。（創立記念日は休日のため、今回は前日11/28に発信しました。）

数学メディアスペース１(2階)の壁に、「ルートメジャー」があります。模造紙をつないで作った5メートルの長さの紙に、メートル(1メートル)からメートル(約1.4メートル)、メートル(約1.7メートル)と、順にメートル(約4.7メートル)、メートル(5メートル)までの目盛りが記されています。3年生1学期の無理数の授業で、クラスごとに1シート作ったルートメジャーです。実際の平方根の大きさ(長さ)を記録することで、ルートの大きさを実感することができました。

“Measure of square root”
There is a “root square measure” on the wall of the Media Space 1 on the 2nd floor.
The scales of the square root of 1 meter to the square root of 25 meters are indicated on the paper that is 5 meters long.
9th grade students made one of them in each class during the 1st term.
Students made this measure and could understand the quantum of square root.

本日11月9日を1109と4ケタの数で表すと、1109は素数です。西暦を含めた20161109は、19×43×24677と素因数分解できるので素数ではありません。

２階数学メディアスペースの「円周率の壁」と名付けた場所に、模造紙に手書きされた楽譜が掲示してあります。これは円周率の3をミ、1をドというように数字を音に割り当て、3.141592・・・がミ、ド、ファ、ド、ソ、高いレ、レと続いていきます。3から始まる113個の音符が五線譜の上に並んでいます。作曲、編曲されたのは、現在立命館守山中学校で数学を教えている長谷川幹(はせがわつよし)さんです。ギターを使って作られたそうで、3連符となっている箇所もあります。この曲はインターネットで実際に聴くことができます。
また、インターネットで検索すると、実は、世界では円周率を元に作られた曲がいくつかあることがわかります。世界には数学を大好きな人が大勢おられますね。
関連URL：http://web.kyoto-inet.or.jp/people/hase_314/pi/pai.htm

“Music of pi”
This is a musical score on the wall at Do★MATH.
3 is assigned to E, 1 is assigned to C, 4 is assigned to F, 1 is assigned to C, 5 is assigned to G, 9 is assigned to D and 2 is assigned to D.
There are 113 digits in this musical score. There is triplet part in the melody.
Hasegawa – san made this melody by using a guitar. He is a math teacher at Ritsumeikan Moriyama Junior High School in Shiga prefecture.
You can hear it on the internet. Also, we can see other melodies about pi in the world!
It is amazing that there are many people who like mathematics very much!