Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース（「数学メディアスペース」）を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。
※こちらのイベントは終了しました。
★3種類まとめて購入すると、送料無料！（2020年9月より当面の間）
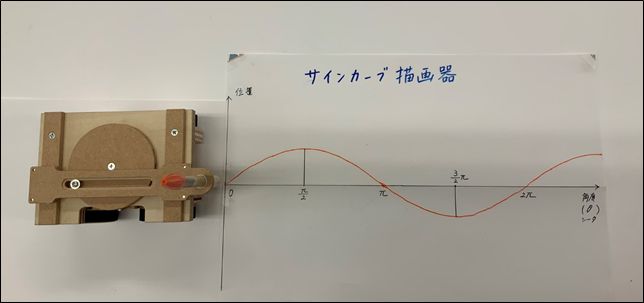
サインカーブ描画器
～“Sine curve drawing machine”～
今日1月27日を3ケタの数で表すと、127は素数です。西暦を含めた20200127は、31と651617、2つの素数の積で表せるので素数ではありません。
今回は、東京理科大数学体験館で作られている「サインカーブ描画器」をご紹介します。2019年8月、玉川聖学院中高数学科の石井俊二さんが来校され、Do★MATH数学博物館をご見学くださいました。そのとき、東京理科大数学体験館の講習で作成された「サインカーブ描画器」をご寄贈くださいました。ありがとうございました。
サインカーブ描画器は、その名前のとおり、木製ミニカーにペンを付けて、歯車を利用し、車が動くのに合わせてサインカーブという曲線を描けるようになっています。
水面の波や、目に見えないですが、音や地震のP波・S波と呼ばれる揺れ、毎日私たちが家庭で使っている電気(正確には交流電圧、交流電流と呼ぶもの)はサインカーブの曲線を描きながら動いています。
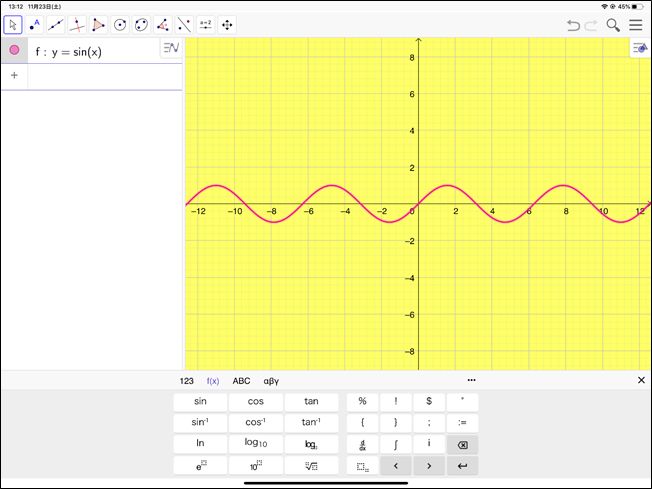
数学の式では、「y=sinx」、「y=sinθ」と表します。GeoGebraで描いたグラフを紹介しますね。
“Sine curve drawing machine”
We will introduce a “Sine curve drawing machine”. It is made by Ishii Shunji san, he teaches math in Tamagawa Seigakuin Middle School. Ishii san came to see our Math Museum and donated it to us.
A “Sine curve drawing machine” can draw a sine curve with pen in tune with a wooden minicar moving using gears.
Waves on the water, sound, P wave and S wave in earthquakes and electricity we use everyday is moving and drawing sine curve.
We write “y=sinx” or “y=sinθ” in math expression. I will show the graph by using a math application “GeoGebra”.
by Tsuyoshi Sonoda (Math Dept.)
下の図は、GeoGebraで描いたサインカーブ曲線です。キーボードで式を入力（画面左上）するだけで、グラフをきれいに描くことができます。パラメータを使って、グラフが描かれる様子（軌跡）をアニメーションで見ることも可能です。
GeoGebraは、幾何、代数、解析を1つに結びつけた動的数学ソフトウェアです。
参考URL: https://sites.google.com/site/geogebrajp/
正多面体は5種類しかない！4
～“Only 5 kinds of Regular polyhedron! 4”～
同志社創立記念日の11月29日を4ケタの数で表すと、1129は素数です。西暦を含めた20191129は、7×19×151813と素因数分解できるので素数ではありません。
今まず、前回のブログで説明したことを簡潔に紹介します。（3）からが今回の内容です。
（1）ある条件をクリアした立体（多面体）は、「オイラーの多面体公式」が成り立っています。
（面の数）＋（頂点の数）－（辺の数）＝ 2 ・・・①
（2）正多面体の面の形をp角形（pは3以上の整数）、頂点に集まる面の数をq（qは3以上の整数）とすると、次の関係が成り立っています。
（ⅰ）（面の数）＝（辺の数）×2/p ・・・②
（ⅱ）（頂点の数）＝（辺の数）×2/q ・・・③
（3）②、③の結果をオイラーの多面体公式①に代入します。
（辺の数）×2/p＋（辺の数）×2/q－（辺の数）＝ 2
両辺を(辺の数)で割って、
2/p＋2/qー1 ＝ 2/(辺の数)
（4）次に、急に不等号が入ります。
2/p＋2/q－1 ＝ 2/(辺の数) > 0
2/p＋2/q－1 ＞ 0
両辺にpqをかけて、式を整理していきます。
2q＋2p－pq ＞ 0
両辺に－1をかけて、
pq－2p－2q ＜ 0
最後に、左辺を因数分解するためのテクニックで両辺に4を加えます。
pq－2p－2q＋4 ＜ 4
（p－2）（q－2）＜ 4
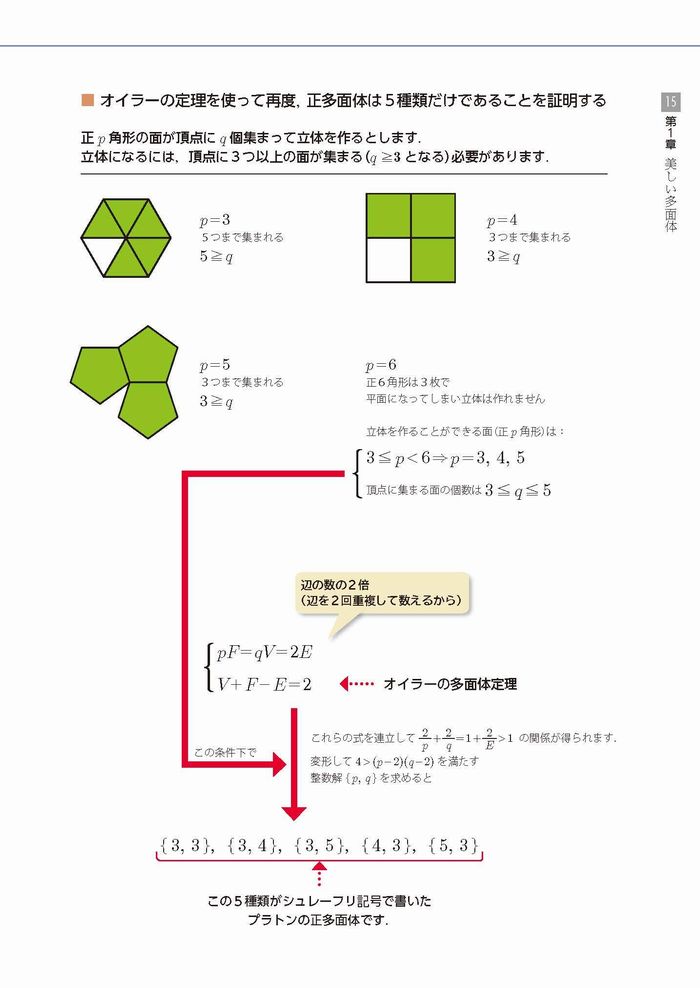
（5）pはp角形のp、qは頂点に集まる面の数のことでした。そして、p、qともに3以上の整数です。この条件でpとqのペアを考えると、
（p、q）＝（3、3）、（3、4）、（3、5）、（4、3）、（5、3）
の5通りしかありません。左のペアから順に、正４面体、正8面体、正20面体、正6面体(立方体)、正12面体を意味しています。
（数学科 園田毅）
“Only 5 kinds of Regular polyhedron! 4”
I will introduce briefly what I explained in the last blog. I will explain the contents from section (3) this time.
(1) “Euler’s polyhedron formula” is established for solids that have some contents.
(the number of faces)＋(the number of vertices)－(the number of sides)＝2・・・ ①
(2) When the shape of regular polygons is “p” (p ≥ 3) and the number of faces is “q” (q ≥ 3),
(ⅰ) (the number of faces) = (the number of sides) × 2/p ・・・ ②
(ⅱ) (the number of vertices) = (the number of sides) × 2/p ・・・ ③
(3) Insert the result of ②, ③ into Euler’s polyhedron formula
(the number of sides)×2/p＋(the number of sides)×2/qー(the number of sides) = 2
Divide both sides of the equality by the number of sides.
(Faces)＋(Vertices)ー(Sides) ＝ 2
2/p＋2/qー1 ＝ 2/(the number of sides)/p>
(4) Here, add an inequality sign to the expression.
2/p＋2/qー1 = 2/( number of sides) > 0
2/p＋2/qー1 > 0
Multiple both sides of the equality by pq and simplify the expression.
2q＋2pーpq > 0
Multiple both sides of the equality by －1
pqー2pー2q < 0
Finally, add both sides of the equality by 4 as a technique to factorization.
pqー2pー2q＋4 < 4
(pー2)(qー2) < 4
(5) p is a p-sided polygon, q is the number of faces gathering at a point. In addition p and q are integer more than or equal to 2. Considering this condition, we have “only 5 kinds” of solutions.
(p, q) ＝ (3, 3), (3, 4), (3, 5), (4, 3), (5, 3)
The answer means tetrahedron, octahedron, icosahedron, cube and dodecahedron from left to right.
Mathematics is wonderful and mysterious because we can know the truth by only calculations even though we don’t have real things in front of us.
by Tsuyoshi Sonoda (Math Dept.)
谷克彦「美しい幾何学」（技術評論社 2019）より
正多面体は5種類しかない！3
～“Only 5 kinds of Regular polyhedron! 3”～
今日11月17日を4ケタの数で表すと、1117は素数です。西暦を含めた20191117も 素数です。
今回は、数学者の谷克彦さんが数学博物館へ寄贈してくださった著書「美しい幾何学」（2019 技術評論社）の中から、正多面体についての内容をご紹介します。
中学1年生で、正多面体は5種類しかないことを学習します。授業では、頂点に着目して図形的に確認しています。詳しくは、ブログ#44『正多面体は5種類しかない！』、#45『正多面体は5種類しかない！2』を見てくださいね。
正多面体が5種類しかないことは、実は「オイラーの多面体公式」を利用して計算で説明できます。式に文字を使い、テクニックを使って式を変形していきます。2回に分けて説明していきます。
（1）まず、「オイラーの多面体公式」を紹介します。ある条件をクリアした立体（多面体）は、
（面の数）＋（頂点の数）－（辺の数）＝ 2 ・・・①
となることがわかっています。例えば、直方体であれば、「6＋8－12 ＝ 2」となっています。
（2）次に、正多面体の性質を考えていきます。正多面体はそれぞれの面の多角形が合同で、頂点に集まる面の数が等しいという特徴があります。面の形をp角形（pは3以上の整数、2角形はできないから）、頂点に集まる面の数をq（qは3以上の整数、2枚で頂点は作れないから）とすると、
（ⅰ）p×（面の数）＝（辺の数）×2
したがって、
（面の数）＝（辺の数）×2/p ・・・②
（ⅱ）q×（頂点の数）＝（辺の数）×2
したがって、
（頂点の数）＝（辺の数）×2/q ・・・③
今回は、面の数、頂点の数、辺の数について３つの式を知りました。次回は、３つの式を使って、正多面体が５つしかない理由を発見しましょう！ 皆さんも考えてみてください。
（数学科 園田毅）
“Only 5 kinds of Regular polyhedron! 3”
Mathematician Tani Katsuhiko san donated his book to our museum and I will introduce the content about regular polyhedrons in his book.
The 7th grade students learn that there are only 5 kinds of regular polyhedron. I explain the reason of the theory graphically thinking about the number of vertex. Please refer to our blog #44“Only 5 kinds of Regular polyhedron! ” and #45 “Only 5 kinds of Regular polyhedron! 2” for details. I will find this theory by calculation using “’Euler’s polyhedron formula”. We make expressions to complete the formula using characters and techniques, so it may be little difficult for junior high school students.
(1) First, this is the “Euler’s polyhedron formula” below. Solids that have some contents always have characters.
(the number of faces)＋(the number of vertices)－(the number of sides)＝2 ・・・①
For example, in the case of the rectangle parallelepiped,
“6+8-12=2” is established.
(2)Next, let’s think about characteristics of regular polyhedron. Regular polyhedron have 2 features, one is that all are regular polygons, the other is that the number of faces gathering at a point are same. When the shape of regular polygons is “p” (p is an integer greater than or equal to 3) and the number of faces is “q” (q is an also integer greater than or equal to 3),
(ⅰ) p×(the number of faces)=(the number of sides) ×2
Then
(the number of faces)=(the number of sides) ×2/p ・・・ ②
(ⅱ) q×(the number of vertices)= (the number of sides)×2
Then
(the number of vertices)= (the number of sides) ×2/p ・・・ ③
We can have 3 relational expressions now.
Let’s get a solution by the next blog and try thinking!
by Tsuyoshi Sonoda (Math Dept.)
数学オープンスペース2「ジョン・スノウ」
～ “Math Open Space 2‘John Snow’.” ～
今日10月9日を4ケタの数で表すと、1009は素数です。西暦を含めた20191009も素数です。
本校数学科では、6つの数学教室と数学ST(教員室)、2つの数学メディアスペースに数学者や科学者の名前をつけています。「数学メディアスペース2」（3階）の名前は「ジョン・スノウ」です。
ジョン・スノウは19世紀のイギリスの医者で、ビクトリア女王にクロロホルムで麻酔をかけた人、そしてまた、調査データを元にロンドン、ソーホー地区でのコレラの流行を止めた人として知られています。彼は同じ時代に活躍したフローレンス・ナイチンゲールと同じく統計学を使って、医学の発展に貢献しました。
当時は、コレラなどの伝染病は汚い空気「瘴気（しょうき）」が発生、感染の元であるとされ、スノウの主張する経口感染説はなかなか受け入れられませんでした。しかし、1854年夏のコレラの流行では、精密な調査の結果、死者はブロードストリートにある井戸の周りの住民と、井戸から離れていても偶然その井戸の水を飲んだ人に限られることがわかりました。スノウはこのデータを元に、井戸の使用を禁止し、コレラの流行を止めることに成功しました。ドイツ人医師ロベルト・コッホ（1843－1910）によって、コレラ菌が発見されるのは1876年のことでした。
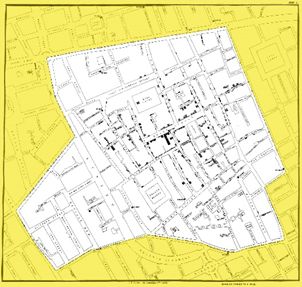ジョン・スノウ（1813－1858）はイギリスの医師。彼が生きた1800年代中頃は、まだ病原菌が発見されていないため、感染源、感染経路が確定されていない病気が多く、コレラもその一つで「死の病」として恐れられていた。1854年夏、ロンドンでコレラが大流行したときも、当初は空気感染が原因であると信じられていた。スノウは死亡者が出た家のマップ（右図）を作成した。ブロード・ストリートの北側に患者が少なく、南側に患者が多かったことから、彼は住民が利用している井戸の水が感染源であることを統計的に突き止めた。
（出典：https://www.ph.ucla.edu/epi/snow/snowmap1_1854.html）
John Snow（1813－1858）was an English physician. He lived in the mid 1800s, and there were many diseases that the sources and routes of infection were not known, because pathogenic bacteria had not been discovered yet. So cholera was feared as a disease of death. In the summer of 1854, at the outbreak of cholera, at first, most people thought air infection was a cause. Snow made the map of the houses where dead people lived. He found there were few sick people in the north of the Broad Street, but many in the south. Then he statistically found out that the pump water residents used was the source of infection.
“The name of the Math Open Space 2 is ‘John Snow’.”
We gave the names of famous mathematicians or scientists to the 6 classrooms, the teacher’s “station” (staff room) and 2 open spaces. The name of “Math Open Space 2” on the third floor is “John Snow”.
John Snow was an English physician who anesthetized Queen Victoria with chloroform and stopped the prevalence of cholera in the Soho area of London using his survey data. He contributed to the advance of medical science in the same period and in the same way Florence Nightingale did, using statistics.
People believed that the origin of infectious diseases like cholera was dirty air, so the oral infection theory Snow asserted was not accepted. But it was found, as a result of the inspection into the prevalence of cholera in the summer of 1854, that many of the dead people lived around the pump on Broad Street or were people who died after drinking the pump water accidentally. Snow prohibited use of the pump using the data and succeeded in stopping a cholera epidemic. It was in 1876 that German physician Robert Koch (1843-1910) identified the cholera vibrio.
by Tsuyoshi Sonoda (Math Dept.)
ｐｐバンドでサッカーボールを作ろう！2
～ “Let’s make a soccer ball using PP bands 2” ～
今日9月19日を3ケタの数で表すと、919は素数です。西暦を含めた20190919は、7、67と43051、3つの素数の積で表せるので、素数ではありません。
今回は、ppバンドで手にのる大きさのサッカーボール（「角切り二十面体」 写真1）を作ってみましょう。もちろんボールとして遊べます。以下に作り方を紹介しますね。ppバンドはホームセンターや通販サイトで購入できます。
（1）ppバンド（幅15mm）を、27.5cm（この内、1.5cmはホッチキスを留める重複部分）に切り、これを6本用意してください。（2）まず、5本のppバンドを、中心に五角形ができるように組み合わせます。ｐｐバンドが交差する部分はそれぞれが互いに内側・外側になるように組み合わせてください。
（3）五角形の頂点をクリップで留めてください。
（写真2）地球に例えると、「南半球」を作っているイメージです。五角形は「南極」にあたります。
（4）残りの1本（白）を他のｐｐバンドにかけていき、1周したらホッチキスで留めてください。
（写真3）白いバンドは「赤道」のイメージです。
（5）「赤道」の上に出てきたｐｐバンドを互いに外側・内側になるようにかけていき、1周したら順にホッチキスで留めてください。
（６）全てのｐｐバンドをホッチキスで留めたら完成です。ホッチキスで留めた部分を他のｐｐバンドの内側に隠すと見栄えがきれいです。
初めて作るときは、40－50分ほどかかります。お家でぜひやってみてくださいね。
（数学科 園田毅）
“Let’s make a soccer ball using PP bands!”
Let’s make a soccer ball (“Truncated icosahedron” figure 1) using PP bands!
Of course we can play using it as a ball. I will introduce the way of making it. We can get PP bands at a do-it-yourself store.
(1) Cut 6 pieces of PP bands (width 15mm) each 27.5cm. (1.5cm of the 27.5cm is to overlap each other for stapling.)
(2) Combine 5 pieces of PP bands which make a pentagon. Combine Parts where 3 PP bands intersect each other alternately.
(3) Keep the vertex of a pentagon by clips. (figure 2) If this soccer ball was the earth, it is like making the southern hemisphere. The part of pentagon is the “South Pole”.
(4) Put the remaining PP bands (white) in and outside the other PP bands alternately and staple it. (figure 3) This is like making an “equator”.
(5) Put 5 PP bands alternately above “equator”. After each PP band has circled the ball, staple it.
(6) It is completed when all PP bands are stapled.
If you put the stapled parts inside the other bands, the ball looks beautiful.
by Tsuyoshi Sonoda (Math Dept.)
