Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース(「数学メディアスペース」)を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。

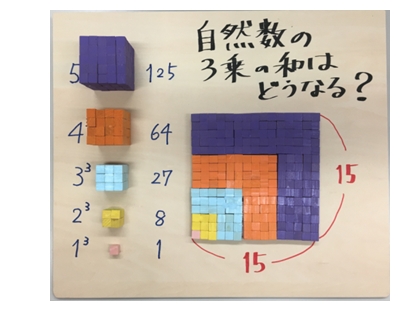
自然数の3乗の和はどうなる?
今日9月19日を919と3ケタの数で表すと、919は素数です。西暦を含めた20170919は1009と19991という2つの素数の積で表されるので、素数ではありません。

13+23+33+・・・+○3 = ?
この合計はいくつになるでしょうか。
上の模型(fig.1)は、○=5 の場合を小さな立方体のピースで表したものです。
すべての小さな立方体の合計は、
13+23+33+43+53
=1+8+27+64+125
=225 (個)
となりますね。
この模型は、○=5 の場合のものなので、5 という数に注目してください。
この模型を平面上に並べると、なんと正方形が出現します! (fig.2)
だから、合計は

13+23+33+43+53
(1+2+3+4+5)2
=152
=225(個)
と求めることができますね。
また、高校では以下の公式を学びます。
{○×(○+1)÷2}²
(数学科 園田)
“What is the sum of natural numbers cubed?”
Let’s talk about the sum of natural numbers cubed.
13+23+33+・・・+○3 = ?
We will think about above expression.
I show the model in the case of n = 5 shown in fig.1.
The sum of small cubes looks like this.
13+23+33+43+53
=1+8+27+64+125
=225 (pieces)
Next, I put the all pieces of cube on a plane, those make a square. (fig.2)
Then we can find the sum of small cubes like this.
13+23+33+43+53
(1+2+3+4+5)2
=152
=225 (pieces)
So we also can get the following formula.
{○×(○+1)÷2}2
by Tsuyoshi Sonoda (Math Dept.)
展開・因数分解パズル3
今日9月7日を907と3ケタの数で表すと、907は素数です。西暦を含めた20170907は823と24509という2つの素数で割り切れるので、素数ではありません。3ケタ以上の素数はプログラムを用いないとすぐには発見できませんね。
展開・因数分解パズルの第3弾です。
 前回のお話で、このパズルが展開・因数分解をイメージしているものであることはおわかりいただけたと思います。
前回のお話で、このパズルが展開・因数分解をイメージしているものであることはおわかりいただけたと思います。
そして、このパズルをより抽象的、象徴的に表したものが面積図や直積表と呼んでいるものになります。
(figure2、figure3)
皆さん、今までは式の中の数値が「+」(プラス)であることを前提にお話をすすめてきましたが、今回は、項がに「-」(マイナス)があるとき(係数や定数項が負の場合)について考えてみます。実は、今までと同じように直積表で解決することができます。「+」(プラス)のときと同じように長さとして考えればよいのです。
x2+5x-14 の因数分解について、実際に解きながら考えてみましょう。
まず、x2 と -14 を直積表の左上と右下に記入します。-14 は負の項なので、直積表では赤い枠で表現しています。
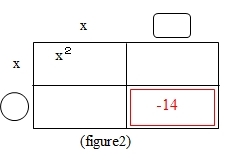 かけて-14になる数を
かけて-14になる数を![]() と
と![]() にあてはめて、右上と左下の合計が+5xになる組を探します。
にあてはめて、右上と左下の合計が+5xになる組を探します。
(+1, -14)、(-1, +14)、(+2, -7)、(-2, +7)の4組をあてはめて、(-2, +7)の組み合わせが正解とわかります。
展開・因数分解が解けることはひらめきや才能と関連があると思っている方もいらっしゃるかもしれません。そうではありません。今の操作を下図に示しました。この問題は最大4回の試行錯誤で必ず正解が出るのです。因数分解パズルで、試行錯誤して正解を見つけることを楽しんでください。(数学科 園田)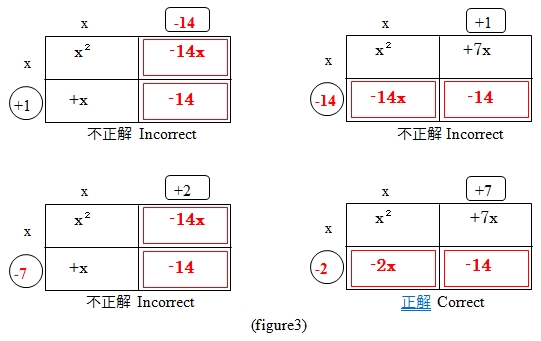
“Expansion & Factorization puzzle 3”
We can use negative numbers as a 2nd step. x2+5x-14 = (x-2) (x+7)
Write “direct product table”, “x2“ and “-14” in the frame, “x” and “x” left and above the upper left box, the same as in example 1.
With trial and error, then we can solve it.
Think of the numbers of ![]() and
and ![]() . The numbers times each other is -14. (+1, -14),(-1, +14), (+2,-7) and (-2, +7) groups are considered. At first, I write +1 and -14 in the blank. Then the amount of term of x is -13x. So I know that +1 and -14 are incorrect.
. The numbers times each other is -14. (+1, -14),(-1, +14), (+2,-7) and (-2, +7) groups are considered. At first, I write +1 and -14 in the blank. Then the amount of term of x is -13x. So I know that +1 and -14 are incorrect.
After several trial and errors, I write -2 and +7. The amount of term of x is +5x. So I know -2 and +7 are correct.
I think that an ability of solving expansion & factorization is not connected with talent of math. We can solve this problem by trial and error less than four times.
Please try and enjoy this puzzle!
展開・因数分解パズル2
明日7月1日を701と3ケタの数で表すと、701は素数です。西暦を含めた20170701は3と23と401という3つの素数で割り切れるので、素数ではありません。(明日は土曜日のため今回は前日6/30に発信しました。)次回の発信は9月7日(木)を予定しています。
 前回、皆さんに直積表を利用して因数分解を理解するパズルを紹介しましたね。今回はその第2弾です。
前回、皆さんに直積表を利用して因数分解を理解するパズルを紹介しましたね。今回はその第2弾です。
このパズルの3種類の板は、
黄 :一辺xの正方形、面積x2
ピンク:一辺がxと1の長方形、面積x
緑 :一辺1の正方形、面積1
です。
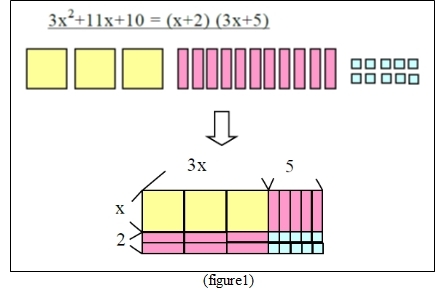
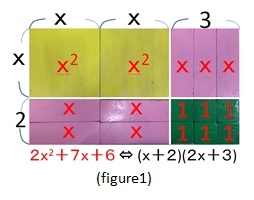
したがって、右の図で、板の種類ごとに面積を表せば、2x2+7x+6となりますし、大きな1つの長方形の面積と考えると、(x+2)(2x+3)となり、2通りの表現で面積を示すことができますね。
これが展開と因数分解の正体です。また、このパズルを簡単に表した(抽象化した)のが直積表です。たすきがけよりも展開・因数分解のしくみが可視化されていますよね。
(数学科 園田)
“Expansion & Factorization puzzle 2”
The last time, I showed “Expansion & Factorization puzzle”. This time, I will explain the structure of expansion & factorization using this puzzle.
Look at the puzzle in “figure1”. “x2” is an area of a square of a side x, “x” is an area of a rectangle with each side of x and 1. “1” is a squares of a side 1. We can say the total area of those pieces is “2x2+7x+6” and can also say “(x+2)(2x+3)”.
This is the true colors of Expansion & Factorization. And “a direct product table” is a model of this puzzle. This model visualizes the structure more clearly than “tasuki – gake”.
展開・因数分解パズル
今日6月19日を619と3ケタの数で表すと、619は素数です。西暦を含めた20170619は7と17と169501でという3つの素数で割り切れるので、素数ではありません。
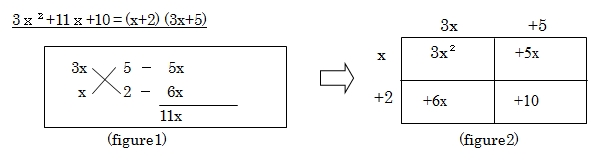
多くの大人の皆さんは中学生、高校生のときに、展開・因数分解をおそらく「たすきがけ」という方法で教えられていると思います。日本の学校では、とくに高校ではほぼたすきがけで教えられています。それは、教科書にはたすきがけ(図1)の方法しか記されていないからで、多くの大人は直積表(図2)を使って教えられた経験がありません。一方、欧米では直積表を使う指導が一般的です。
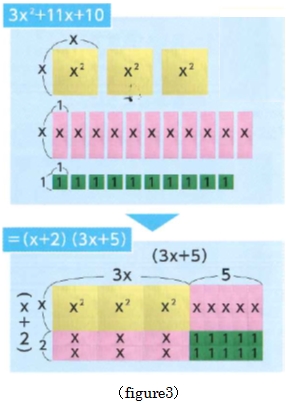 右の図を見てください。直積表を使って考えると、この図3のように因数分解を長方形のタテとヨコの長さとして認識できるからです。
右の図を見てください。直積表を使って考えると、この図3のように因数分解を長方形のタテとヨコの長さとして認識できるからです。
Do★MATHには、展開・因数分解パズルがあります。黄○枚、ピンク○枚、緑○枚を使って1つの長方形を作ろうという課題が提示されていて、楽しみながら展開・因数分解の概念を理解することができます。
大人の皆さんも生徒・学生の皆さんもこのパズルを楽しんでください。
(数学科 園田)

“Expansion & Factorization puzzle”
Many people have studied expansion & factorization by using fig.1, “tasuki – gake” in Japan, especially in high school. Because Japanese official textbooks authorized by the Japanese government describe only one way of teaching fig.1, many Japanese teachers do not know the way of using fig.2. But many people in Europe study expansion & factorization by using fig.2, “a direct product table”
Please check fig.3.
When you think about a factorization problem by using a direct product table, you can recognize numbers and expressions as length and area of a rectangle.
We have Expansion & Factorization puzzle in our Do★MATH. You can see the meaning of expansion and factorization playing with this puzzle.
Let’s try it together!
しきつめ
今日6月13日を613と3ケタの数で表すと、613は素数です。西暦を含めた20170613は113と178501という2つの素数で割り切れるので、素数ではありません。
 皆さんは「しきつめ」を知っていますか。1種類または数種類の合同な図形で平面をすきまなくしきつめていくことです。正六角形をしきつめたハニカム構造もその一つです。1種類の多角形でしきつめるときは、どんな多角形でもできるわけではありません。しかし、三角形と四角形はうまく並べると、必ず平面をしきつめることができます。これをデザインとして応用したのがエッシャー(1898 – 1972)です。彼がしきつめデザインの作品を多く発表したので、しきつめは「エッシャー図形」として有名になりました。自分で書くときは、平行四辺形やひし形から模様を書き始めると作りやすいです。
皆さんは「しきつめ」を知っていますか。1種類または数種類の合同な図形で平面をすきまなくしきつめていくことです。正六角形をしきつめたハニカム構造もその一つです。1種類の多角形でしきつめるときは、どんな多角形でもできるわけではありません。しかし、三角形と四角形はうまく並べると、必ず平面をしきつめることができます。これをデザインとして応用したのがエッシャー(1898 – 1972)です。彼がしきつめデザインの作品を多く発表したので、しきつめは「エッシャー図形」として有名になりました。自分で書くときは、平行四辺形やひし形から模様を書き始めると作りやすいです。
 ニューヨークの数学博物館MOMATHが、しきつめ用のいろんな形のパーツを販売しています。先日、うさぎとさるのパーツを買ってきました。 数学ステーション(数学科教員室)入口のホワイトボードに貼ってあります。
ニューヨークの数学博物館MOMATHが、しきつめ用のいろんな形のパーツを販売しています。先日、うさぎとさるのパーツを買ってきました。 数学ステーション(数学科教員室)入口のホワイトボードに貼ってあります。
ぜひチャレンジしてください。
(数学科 園田)
“Tessellation”
Do you know tessellation?
A tessellation is the making of a tile plane using one or more geometric shapes.
You may have seen honeycomb structures like the figure. We can make of a tile plane using triangles and quadrangles. Escher (1898 – 1972) was famous for tessellation designs.
MoMATH sells pieces that we can use to make tessellation on a flat surface. I bought pieces in the forms of a rabbits and horses. Those are on the wall near the Math station (math teacher’s room) on the 3rd floor.
Please come to Do★MATH and try them!





