Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース（「数学メディアスペース」）を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。
★3種類まとめて購入すると、送料無料！（2020年9月より当面の間）
サイクロイドすべり台2
本日9月19日を919と3ケタの数で表すと、919は素数です。西暦を含めた20180919は、3、11、そして611543という素数で割れるので、素数ではありません。
前回のブログでは、サイクロイドという曲線が急に出てきて、見たことのない式や記号（θ シータ）が入っていて難しく感じられたと思います。今回は、皆さんにサイクロイド曲線をわかりやすくご説明します。
サイクロイドは、一般的に、円が直線の上を転がったとき、円周の上の1点が動く模様を描いた曲線です。自転車のタイヤについているマークが、タイヤが道路を転がるのに合わせて動いていく様子をイメージするとわかりやすいと思います。
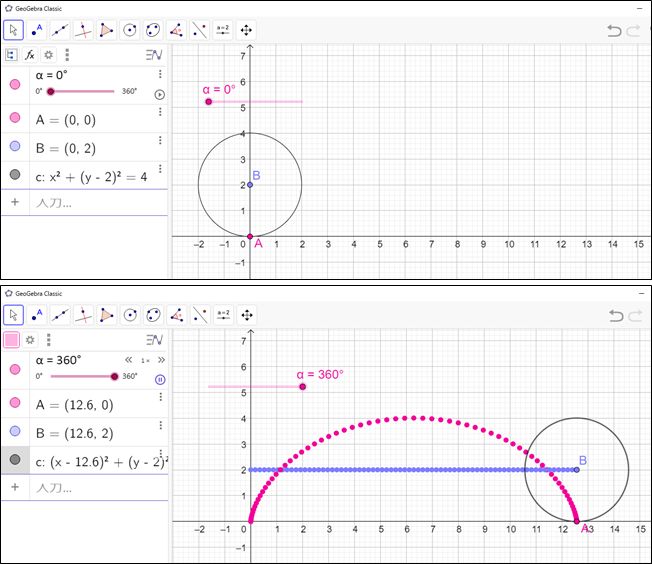
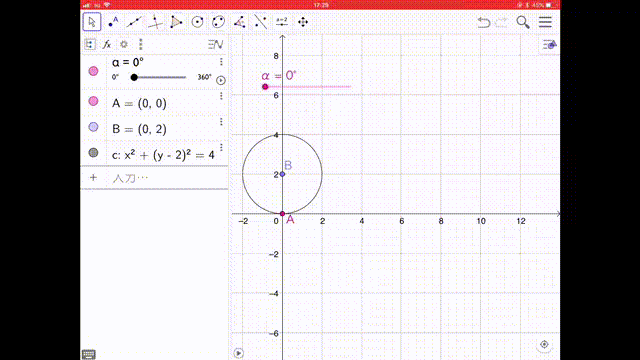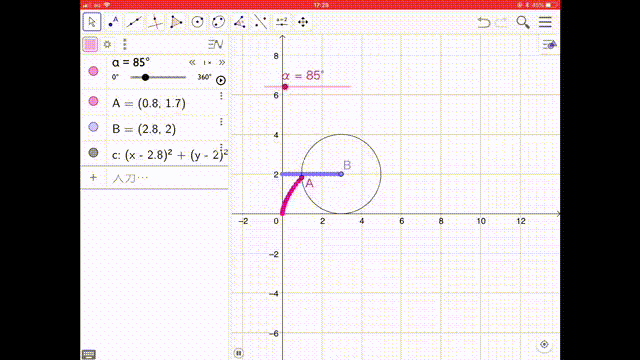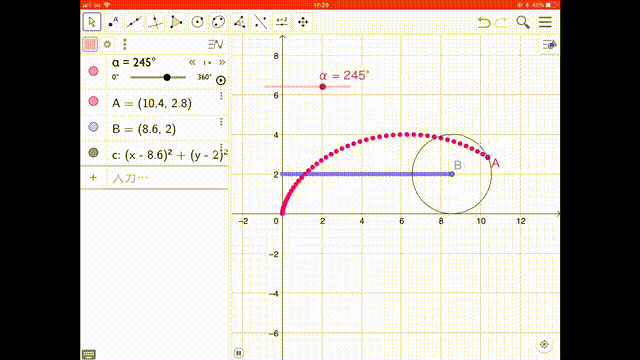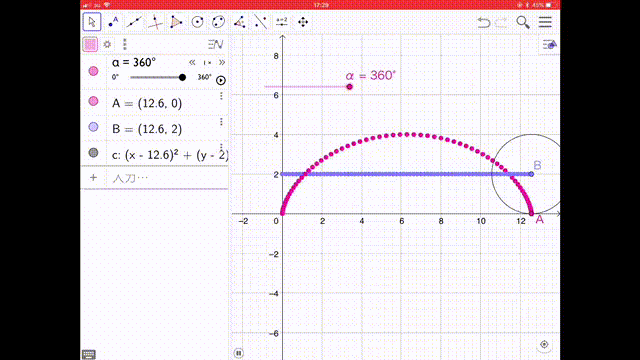
今回は、GeoGebra というグラフソフトで描きました。このグラフでは、動く点(動点 どうてん)は原点からスタートしています。動画で、円が動くとともにサイクロイド曲線ができていく様子を見てください。サイクロイドすべり台は、このグラフの上下をひっくり返したラインの形になっています。
2015年に、中学3年生の奈須隼大さんが自由研究でいろいろな関数をまとめて作成された「関数の入口」という冊子にもサイクロイドが紹介されていました。
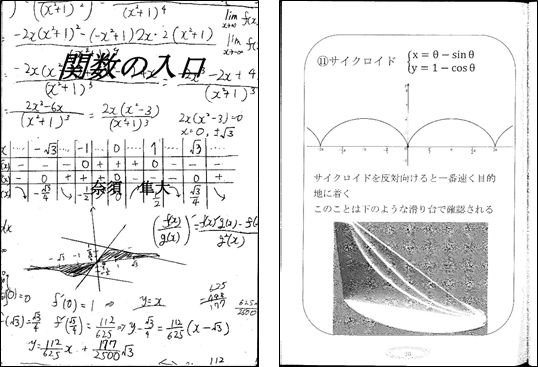
サイクロイド曲線は1年生の授業で、10円玉はタイヤ、定規は道路のイメージで10円玉の1ヶ所に鉛筆を当て、定規の上を転がして描いていきます。円もそうなのですが、点がある規則で動くと、きれいな線ができますね。
（数学科 園田）
“Cycloid slide 2”
You may feel that it was difficult to read the last blog and to see the unknown mathematical symbols in the expression of cycloid.
We want to explain how to understand cycloid curve in this blog.
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line generally.
It is easy to understand if you imagine that a mark on a wheel of a bicycle rolls on a road.
We wrote a cycloid using an application called GeoGebra. The moving point of this graph starts from origin. Please check this movie. It will be the graph of cycloid with a circle moving. This cycloid slide is a opposite shape of this graph. In 2015, a 9th grade student Nasu hayato san wrote a book “The Entrance of the Function” in his research work and he introduced a cycloid graph.
In our 7th grade student’s class, they write cycloid graphs using a pencil along one point of a 10-yen coin rolling on the scale. We can see beautiful lines with the point moving according to the rules like a circle.
by Tsuyoshi Sonoda (Math Dept.)
サイクロイドすべり台
本日9月7日を907と3ケタの数で表すと、907は素数です。西暦を含めた20180907は、36×19×31×47と素因数分解できるので、素数ではありません。
今回、ご紹介するのは、木製の「サイクロイドすべり台」です。スタートとゴールを同じにした3つのコースにビー玉を同時に転がして実験します。直線、放物線（2次関数）、サイクロイドと呼ばれる曲線の3コースでそのスピードを競います。
結果は・・・サイクロイド曲線のルート(写真で最も手前のライン)を通ったビー玉が最も速くゴールに到達します。ジェットコースターのコースはできるだけスピードが出るようにサイクロイド曲線をもとに設計されていて、サイクロイド曲線は「最速降下曲線」とも呼ばれます。
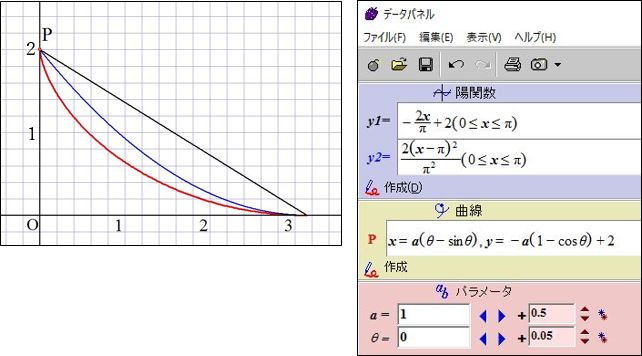
次に、写真で実物とその設計図面（グラフ）を紹介します。GRAPESというソフトで、高さ2、水平距離3.14（円周率）という設定でグラフを描きました。実際の高さは50cmです。サイクロイド曲線の式は表現が難しくて、媒介変数θ（シータ）というものを使って、この図の場合は、
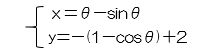
というふうに表されます。
このすべり台はリスーピアはじめ各地の科学館にありますが、本校には現在高校生のご家族の方が2015年に作ってくださった模型もあります。
（数学科 園田）
We will introduce our wooden “Cycloid slide”. We can experience this by rolling three marbles at the same time on the three courses that have same start point and goal point. We research which marble rolls most quickly on the courses of a linear function, a parabola and a cycloid.
The result is that the marble on a cycloid line reaches to the goal first. Courses of roller coasters are designed based on cycloid curve so that those run as fast as possible and a cycloid curve is called “a brachistochrone curve”.
Next, we will introduce the real thing and its blueprint (graph). We draw graphs where the height is 2 and the width is 3.14 (π). Real height is 50 centimeters. It is difficult to express cycloid curves, so we express
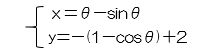
using parameter θ.
There are “Cycloid slides” exhibited in many science museums of Japan. We also have another model our student’s grandfather made in 2015.
by Tsuyoshi Sonoda (Math Dept.)
数学ＳＴ「オイラー」
本日7月9日を709と3ケタの数で表すと、709は素数です。西暦を含めた20180709は32×101×1492と素因数分解できるので、素数ではありません。
今回は、数学ＳＴ（ステーション）入口に掲示している「オイラー」のパネルと説明文をご紹介します。数学ＳＴは数学科教員室のことです。
レオンハルト・オイラー（1707-1783）は、パネルにも書いたように、たいへん多くの業績を残した数学者です。今回は、彼の功績の中から、1つだけ紹介します。
値は、約1.644934だとわかっていたのですが、円周率πが分数の計算の答えに含まれているなんてとても不思議な感じがしませんか。
現在、この式は「リーマンゼータ関数」（正確には、ゼータ関数のｓ＝2の場合）と呼ばれています。ゼータ関数の研究は、証明されると100万ドルの賞金がもらえるミレニアム問題の1つ「リーマン予想」の解決につながると言われています。
今回は、聞いたことのない用語がいくつも出てきたかもしれません。ブログを読んでくださった皆さんの中から、ゼータ関数を研究してリーマン予想にチャレンジする方が出てくることを期待しています。
（数学科 園田）
Leonhard Euler（1707－1783）was a pioneering Swiss mathematician and physicist. He was born in Basel Switzerland. He worked at the Russian Academy of Sciences and Prussia Academy of Sciences. He was the first person who used“y=f(x)”as a function. He wrote more than 800 papers after he lost his sight in 1766. In 1736, Euler presented a solution to the problem known as the Seven Bridges of Koenigsberg. There are many theories he discovered like“Euler’s polyhedron formula”. Especially “Euler’s identity ｅｉπ＋１＝０” is most well-known. It is introduced in “Hakase no aishita suushiki”, a Japanese popular novel.
“The name of the math staff room is ‘Euler’.”
We will introduce the panel of “Leonhard Euler” and a document to explain the panel this time.
Leonhard Euler (1707 – 1783) was a mathematician who had many achievements. We will introduce one episode about him.
Euler had a solution to the problem “the sum of all reciprocal numbers of square
This problem was called the “Basel Problem“ at that time. The sum of the series approximately equal to 1.644934. It may be mysterious that the solution of sum of fractions contained pi.
We call this equation “The Riemann zeta function or Euler-Riemann zeta function” now. Exactly it is the case that “s=2” in the Riemann zeta function.
Research of the Riemann zeta function will solve “Riemann hypothesis” that is one of the Millennium Prize Problems. A person who can solve this Millennium Prize Problems get a prize of one million US dollars.
You might see the many words you have never heard this time. I expect that someone who read this blog might research the Riemann zeta function and challenge to solve the Riemann hypothesis.
by Tsuyoshi Sonoda (Math Dept.)
数学教室6「アルキメデス」
本日6月13日を613と3ケタの数で表すと、613は素数です。西暦を含めた20180613は3×379×177493と素因数分解できるので、素数ではありません。
今回は、数学6教室入口に掲示している「アルキメデス」のパネルと説明文をご紹介します。
アルキメデスと言えば、黄金の王冠のエピソードが有名です。
王様から、黄金の王冠が本物か偽物かを見つける方法を尋ねられて、アルキメデスはずっと考えていました。正確に体積を測ることができれば、密度の違いから王冠が純金なのか銀が混ぜられた偽物なのかわかりますが、王冠は直方体のように計測できる形状ではないので、その正確な体積を測るのはとても難しいことでした。それで、アルキメデスが考え出したのが次の方法だと言われています。
王冠と同じ重さの純金をてんびんでつりあわせた後、そのまま水中へ移動します。王冠が本物であれば水中でもつりあったままですが、王冠に銀が混じっていると体積が純金より大きくなるため、その結果浮力も純金より大きくなり、水中のてんびんでは王冠が上へ傾くことになります。
ある日、アルキメデスは風呂に入ったところ、水が湯船からあふれるのを見て、その瞬間、この考え「アルキメデスの原理」のヒントを発見しました。このとき、浴場から飛び出たアルキメデスは「ユリーカ」（わかった）と叫びながら裸で走っていったと言われています。
この他にも、アルキメデスは多くの発明、発見をしています。
（数学科 園田）
Archimedes（287BC－212BC）was an Aincient Greek mathematician, physicist, and astronomer. He founded the principal of buoyancy in a bath and took to the street crying “Eureka!”. He used a polygon with 96 sides to calculate the value of Pi between 223/71 and 22/7(3.14…). He also calculated solid content and the surface area of a sphere, and found both of them were 2/3 of a column circumscribing the sphere. He was killed by a Roman soldier while thinking of a mathematical problem in Syracuse（the islands of Sicily）. His portrait is on the Fields Prize medal.
“The name of math classroom 6 is ‘Archimedes’.”
We will introduce the panel of “Archimedes” and a document to explain the panel this time.
The episode of a gold crown about Archimedes is famous.
Archimedes was thinking about a question that was the way to find if the gold crown is a genuine article or not. When we can know the volume of the crown exactly, we find that the crown was made of only gold or it was mixed with silver. But the crown was not a rectangular, so it was difficult to measure the volume exactly. Then Archimedes had an idea to find out the following way.
First, we measure the crown and the gold that has same weight as the crown on a balance. Second, we put them in water to check that the crown is a genuine article, with the balance. If the crown was mixed with silver, the volume of the crown would be bigger than the gold. As a result, the crown would move upper on the balance in the water.
One day, when he took bath and he saw water overflowing from the tub, he found the hint of Archimedes’ principle. Then he cried “Eureka” and ran out of his house and ran naked in the street.
Besides this, he had many discoveries and inventions.
by Tsuyoshi Sonoda (Math Dept.)
ハノイの塔
本日5月23日を523と3ケタの数で表すと、523は素数です。西暦を含めた20180523は3×11×611531と素因数分解されるので、素数ではありません。
皆さんは、「ハノイの塔」というゲームを知っていますか。世界中で人気のあるゲームです。今回は、このゲームと数学の関連をご紹介します。もちろん、「ハノイの塔」は数学メディアスペースに置いてあります。
このゲームは、以下のルールに従って、すべての円盤を最初の杭（くい）から残り２本どちらかの杭に移動させられれば完成です。
(1)３本の杭と、中央に穴の開いた大きさの異なる複数の円盤がある。
(2)最初は、すべての円盤が左端の杭に小さいものが上になるように順に積み重ねられている。
(3)円盤を１回に１枚ずつどれかの杭に移動させることができるが、小さな円盤の上に大きな円盤を載せることはできない。
何度かやっているうちに、コツがわかってきます。写真では円盤は５枚ですが、最初は３枚からスタートして、最短何回で他の杭に移せるか数えていきましょう。3枚の場合の最短回数は7回です。その後、円盤を１枚ずつ増やしながらやってみましょう。まずは円盤が何枚のときは最短何回で完成することができるか調べてみましょう。実は、このゲームには数学的な規則性や法則があります。
（○＋１）枚を移動する最短回数 ＝ ○枚を移動する場合の最短回数 × 2 ＋ 1（回）
（２）円盤○枚を移動する場合の最短回数は、○を使って表すことができます。
○枚を移動する場合の最短回数 ＝ 2○－1（回）
「ハノイの塔」は、フランスの数学者リュカ（1842－1891）が1883年に創作、発売したゲームです。日本でも20世紀初めに紹介されて以来、楽しまれています。ルールが単純なので、誰でも気軽に遊べますね。同中学びプロジェクト（放課後特別企画）では、写真のように円盤を折り紙で代用して楽しみました。
（数学科 園田）
“Tower of Hanoi”
Do you know “Tower of Hanoi”? This game is popular all over the world. We will introduce the connection between this game and mathematics. Of course we have this in our math space.
The goal of the game is to move all the disks on one entire stack to another rod, with the rules below.
(1)Only one disk can be moved at a time.
(2)Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack.
(3)No disk may be placed on top of a smaller disk.
This is the best way to solve the game. Let’s start the game using only 3 disks. The game can be solved in 7 moves with 3 disks. Then please try increasing one by one.
the minimum number of times to move (○+1)
= the minimum number of times to move ○ × 2 + 1
(2)We can express the minimum number of times to move ○ using ○.
the minimum number of times to move (○+1) ＝2○ – 1
“Tower of Hanoi” is the game which French mathematician Lucas (1842-1891) made and sold in 1883. It was also introduced in Japan at the beginning of the 20th century and became popular. The rules of this game are easy, so anyone can play it. We enjoyed it using origami instead of disks as in the photo at an extra program “Do-chu Manabi Project” that we did after school.
by Tsuyoshi Sonoda (Math Dept.)
