Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース(「数学メディアスペース」)を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。

正多面体は5種類しかない!
~”Only 5 kinds of Regular polyhedron”~
本日2月23日を3ケタの数で表した223は素数です。西暦を含めた20190223は、2161×9343と素因数分解できるので、素数ではありません。
多角形で囲まれた立体を多面体と言います。その中で、1種類の正多角形(正三角形、正方形、正五角形・・・)の面で作られたものをとくに「正多面体」と呼んでいます。正多面体はたった5種類しかありません。正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体です。そのうち、正四面体、正八面体、正二十面体は、正三角形の面でできています。立方体(正六面体)は正方形で、正十二面体は正五角形でできています。写真は、左から、正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体です。2階数学メディアスペースに模型を展示しています。

正六面体は普通のサイコロ、ルービックキューブなどよく見かけると思います。正八面体は映画「天空の城ラピュタ」で、ラピュタの中心部にある巨大な「飛行石」の形と言えば思い浮かぶ方が多いのではないでしょうか。
これらの正多面体は、かなり昔から知られていたと言われています。プラトン(紀元前427-紀元前347)が彼の著書「ティマイオス」で正多面体について触れています。それで、正多面体は「プラトンの立体」とも名付けられています。
正多面体が5種類しかないことは、それぞれの正多面体の角が正〇角形何枚でできているかを考えてみるとわかってきます。
①正四面体 - 正三角形が3枚
②正六面体 - 正方形が3枚
③正八面体 - 正三角形が4枚
④正十二面体 - 正五角形が3枚
⑤正二十面体 - 正三角形が5枚
ヒントは2つです。1つ目は、正多角形が3枚以上でないと立体の角を作ることはできません。もう1つは、角に集まる正多角形の角度の合計は360度未満でなければなりません。ここから先は、ぜひ考えてみてください。
(数学科 園田)
“Only 5 kinds of Regular polyhedron!”
Polyhedron are solids with flat polygonal faces. There are special polyhedron called ‘Regular polyhedron’ which are made with the same regular polygons with the same number of faces meeting at each vertex. Only 5 kinds of solids meet these criteria. Tetrahedron, cube, octahedron, dodecahedron and icosahedron. Those are found on the second floor in our math space.
You will often see a cube as a dice and a Rubik’s cube. I think you saw a octahedron as a big Levistone in the Japanese movie ‘Castle in the Sky’.
People in old times knew about regular polyhedron. Plato described about them in his book ‘Timaeus’. So we also call regular polyhedron a Platonic solid.
We can explain that there are only 5 kinds of regular polyhedron by thinking how the structure of the vertices of regular polyhedron are made.
(1)Tetrahedron – 3 regular triangles
(2)Cube – 3 squares
(3)Octahedron – 4 regular triangles
(4)Dodecahedron – 3 regular pentagons
(5)icosahedron – 5 triangles
We have two hints. One is that we can make veritices by more than 3 polygons. The other is that the sum of angles of regular polygons gathering at a point are less than 360 degrees.
Let’s think beyond here!
by Tsuyoshi Sonoda (Math Dept.)

茶色のチョコとホワイトチョコの並べ方はどうなる?
本日1月31日を131と3ケタの数で表すと、131は素数です。西暦を含めた20190131は13×281×5527と素因数分解できるので、素数ではありません。
茶色のチョコとホワイトチョコのブロックが2つずつ、合わせて4つあると考えてください。
チョコを見ないままで4つを下の図のように並べると、同じ色が隣りあうときと、茶色と白が
交互に並ぶときがありますね。
それぞれの場合の確率はどうなると思いますか。同じでしょうか、それとも違うでしょうか。
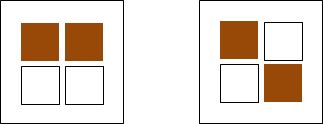
正解は、「2:1で同じ色が隣りあうときが多い」です。確率はどちらも同じだと思った人が多いのではないでしょうか。
直線に並べた場合で考えるのがコツです。6通りの可能性が考えられます。
①茶-茶-白-白 隣りあう
②茶-白-茶-白 繰り返す
③茶-白-白-茶 隣りあう
④白-茶-茶-白 隣りあう
⑤白-茶-白-茶 繰り返す
⑥白-白-茶-茶 隣りあう
となり、隣りあうほうが交互になることより2倍多いのです。
(数学科 園田)

“What is the probability of arranging 2 kinds of chocolate?”
There are 4 pieces of chocolate, 2 pieces are brown and 2 pieces are white.
When those are mixed without looking them, there are 2 cases. One case is that same color chocolate pieces are next to each but the other, other case is that different color chocolates alternate.
What do you think the probability of each case is? Is the probability of each case the same or different?
The answer is that probability of the case that the same color chocolates are next to each other is bigger than the other case.
This is the hint to think the case that the chocolate pieces follow in the line. There are 6 patterns.
(1) Brown – Brown – White – White
(2) Brown – White – Brown – White
(3) Brown – White – White – Brown
(4) White – Brown – Brown – White
(5) White – Brown – White – Brown
(6) White – White – Brown – Brown
So probability of the case that same color chocolates are next to each other is 2 times bigger than the case that different color chocolates alternate.
by Tsuyoshi Sonoda (Math Dept.)

スーパーカミオカンデ
本日1月9日を109と3ケタの数で表すと、109は素数です。西暦を含めた20190109は79と255571の積で表せるので、素数ではありません。
本校は、「同中学びプロジェクト」という特別課外授業で、旧神岡鉱山(岐阜県飛騨市)に作られた宇宙線研究施設「スーパーカミオカンデ」を2014年12月に初めて中学生とともに訪問しました。その後も、2017年12月、2018年7月と訪問しました。
 2018年度の自由研究で、田中将悟さん(2年生)はスーパーカミオカンデの模型(写真)を作りました。スーパーカミオカンデが鉱山の中に作られていること、観測用純水タンクの中に、光電子増倍管がしきつめられていることがよくわかります。
2018年度の自由研究で、田中将悟さん(2年生)はスーパーカミオカンデの模型(写真)を作りました。スーパーカミオカンデが鉱山の中に作られていること、観測用純水タンクの中に、光電子増倍管がしきつめられていることがよくわかります。
田中さんは、9月の放課後に実施した「スーパーカミオカンデゼミ」でこの模型や研究施設の写真を参加者に見せながら、スーパーカミオカンデの構造をわかりやすく説明してくれました。この模型は、立志館2階、数学メディアスペース(MS)の陳列ケースに展示してあります。
また、スーパーカミオカンデ見学に関する展示を立志館入口から数学教室へ上がる階段の途中2か所に掲示してあります。1か所は2018年7月に訪問した報告原稿、もう1か所はスーパーカミオカンデに関する新聞記事などを紹介しています。
ぜひ一度ご覧になってください。
(数学科 園田)

“Super-Kamiokande”
We visited Kamioka Observatory and Super-Kamiokande in Hida city, Gifu prefecture in December 2014 for the first time. We also visited there in 2017 and 2018.
Tanaka Shogo san (8th grade) made a model of Super-Kamiokande as his research work during this summer vacation. We can see that Super-Kamiokande is made in a mine site and has the photo-multiplier tubes on the wall of the tank.
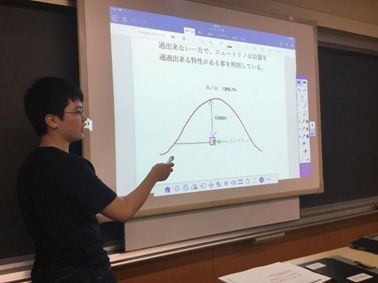 Tanaka san explained clearly the construction of Super-Kamiokande showing the model and photos at an special program, “Do – chu Manabi Project”, after school in September. This model is exhibited in a display case on the second floor in our math space.
Tanaka san explained clearly the construction of Super-Kamiokande showing the model and photos at an special program, “Do – chu Manabi Project”, after school in September. This model is exhibited in a display case on the second floor in our math space.
Also we put display items at two spaces on the wall at the middle of the stairs in Rishikan building. A report of our visiting Super-Kamiokande is on a wall and documents including articles in the newspaper on the other.
Please check them!
by Tsuyoshi Sonoda (Math Dept.)

ソーマキューブ
本日10月31日を1031と4ケタの数で表すと、1031は素数です。西暦を含めた20181031は13×31×50077と素因数分解できるので、素数ではありません。
 ソーマキューブは、小さな立方体(木製)を3~4個くっつけたパーツを組み合わせて、27個(3×3×3)でできる大きな立方体(キューブ)を完成させる遊びです。組み立て方は480通りもあり、ソーマキューブはとても奥が深いパズルです。本校の課外特別授業「同中学びプロジェクト」では、小さな立方体から自分でパーツを作り、キューブを組み立てながら、できるだけ多くの組み立て方を考えていきます。
ソーマキューブは、小さな立方体(木製)を3~4個くっつけたパーツを組み合わせて、27個(3×3×3)でできる大きな立方体(キューブ)を完成させる遊びです。組み立て方は480通りもあり、ソーマキューブはとても奥が深いパズルです。本校の課外特別授業「同中学びプロジェクト」では、小さな立方体から自分でパーツを作り、キューブを組み立てながら、できるだけ多くの組み立て方を考えていきます。
デンマークの詩人でデザイナーのピート・ハイン(1905-1996)は、ドイツの物理学者ハイゼンベルク(1901-1976)の量子力学の講義中に、「ソーマキューブ」を考えました。講義の中の「空間を多数個の立方体に切り分ける」という彼の話から、ハインはこのアイデアを思いついたのです。それは、「4個以下の立方体を接続してできる立体のうち、凹凸のあるブロックだけを全て使って1個の大きな立方体を作ることができる」というものです。
ソーマキューブは、最初は大人のパズルとして考案されましたが、現在は子どもの知育遊びとして活用されています。ソーマキューブの7つのパーツに決まった色を塗って、普通の積み木遊びとしても楽しまれています。
パズルを完成するヒントを一つ教えましょう。T字形(黄色)のパーツは必ず大きな立方体の一辺になります。まだの方はぜひ一度チャレンジしてみてください。
(数学科 園田)

“Soma cube”
We will introduce “Soma cube”. The Soma cube is a game that uses 7 pieces made of unit cubes into a 3×3×3 cube. Each piece is made of 3 or 4 unit cubes. The number of assembling methods are 480. Our students make 7 pieces from unit cubes themselves, and think of the number of assembling methods through putting up at an extra program “Do – chu Manabi Project” that we did after school.
Danish poet, designer Piet Hein (1905-1996) invented it during a lecture on quantum mechanics conducted by German physicist Werner Heisenberg (1901-1976). Piet Hein had an idea from Heisenberg’s story, “we divide space from many cubes”. The idea is “we can make a big cube using pieces that have unevenness and were made of 3 or 4 unit cubes.
The Soma cube was invented as a puzzle game for adults, now we use the game for activity for children. There are different colors for each piece, so people can enjoy normal building blocks games.
I will show you a hint to complete this puzzle. The T-shaped piece (yellow) is always a side of big cube. If you have ever not tried it, please check it out!
by Tsuyoshi Sonoda (Math Dept.)

糸かけ曼荼羅
本日10月9日を1009と4ケタの数で表すと、1009は素数です。西暦を含めた20181009は3×59×113×1009と素因数分解できるので、素数ではありません。
糸かけ曼荼羅は素数の性質を利用したデザインです。シュタイナー教育で使われたことが始まりとされています。(参考サイト:日本糸曼荼羅協会 https://www.itomandala.com/)
 板の上に円周上に釘を打ち、素数ごとに数色の糸をかけていくと、神秘的ですてきな作品ができ上がります。
板の上に円周上に釘を打ち、素数ごとに数色の糸をかけていくと、神秘的ですてきな作品ができ上がります。
今回は、48本のピンで作る方法を紹介します。まず23番目ごとに、時計回りに糸をかけていきます。糸はどのピンとも重複することなく、糸を最初にかけたピンに戻ってきます。その後、19、17、13、11、7、5番目ごとに糸をかけていきます。
これらの数が素数であること、正確には、48とこれらの数の最大公約数が1であることがポイントです。
 集中しないと糸をかける場所を間違えてしまいます。色の選択、順序は自由です。
集中しないと糸をかける場所を間違えてしまいます。色の選択、順序は自由です。
現在、中学2年生の亀井優快さんは、小学生のときに、自作の素敵な糸かけ曼荼羅を本校に寄贈してくださいました。彼の作品が数学1教室前の廊下に展示してあるので、ぜひご覧になってください。(数学科 園田)
 “String – Mandala” is a design that supplies the nature of prime numbers. It was started when it was used at Waldorf education. We can make mysterious lovely works using some kind of color threads on nails put around the circumstances on the board.
“String – Mandala” is a design that supplies the nature of prime numbers. It was started when it was used at Waldorf education. We can make mysterious lovely works using some kind of color threads on nails put around the circumstances on the board.
We will introduce how to make “String – Mandala” using 48 nails. First, we wind a thread clockwise at each 23rd nail. A thread goes back to the first nail not duplicating any nails. After that, we wind threads at each of the 19th, 17th, 13th, 11th, 7th, 5th nails.
It is important the numbers are prime numbers. Exactly, GCD between these numbers and 48 is 1. If we do not concentrate to work, we will mistake the point to put a thread. It is free to choice colors and orders of threads.
Kamei Yukai san (8th grade) donated self – made “Itokake – Mandala” to our school. We exhibit his work in the hallway before math classroom 1. Please check it.
by Tsuyoshi Sonoda (Math Dept.)






