Do★Math 数学博物館 Mathematics Museum

今日9月7日を3ケタの数で表すと、907は素数です。西暦を含めた20190907は11×11×166867と素因数分解できるので、素数ではありません。

前回、工作用紙で自作したサッカーボール（「角切り（かくぎり）二十面体」という「半正多面体」の1つ）をご紹介しましたが、小包の包装などに使われているppバンドからも作ることができます。
写真1を見てください。球体の表面に空いているすき間は正五角形です。そして、ppバンドを見ると、正五角形の各辺（青い線）とその頂点どうしを結ぶ線（緑の線）が正六角形を作っているのがおわかりになるでしょう。
ppバンドで作ったこの立体の不思議なところは、もう1種類の半正多面体に見えるところです。
写真2を見てください。ｐｐバンドの真ん中にマジックで線を引いていきます。こうすると、この立体は正五角形と正三角形でできた半正多面体に見えることがわかりますね。これは「二十・十二面体」と呼んでいる半正多面体です。
角切り二十面体（写真1）と二十・十二面体（写真2）、この2つの半正多面体は少し違いがあります。角切り二十面体の辺は、正五角形と正六角形にはさまれた辺（青い線）と2つの正六角形にはさまれた辺（緑の辺）、2通りの場合があります。一方、二十・十二面体は、すべての辺が正五角形と正三角形にはさまれています。それで、二十・十二面体は、半正多面体の中でも特別に「準正多面体」と呼ばれて区別されています。
（数学科 園田毅）

“Let’s make a soccer ball using PP bands 1”
I introduced a solid of a soccer ball made by working paper and it is called a “Truncated icosahedron” which is one type of ”semi – regular polyhedron” in the last blog. Today, I will show that we can also make the solid using PP bands. Please look at figure 1. The shape of holes on the surface of the sphere is a regular pentagon. If you check the PP bands, you will know that each side (blue lines) of regular pentagons and each other side (green lines) connecting their vertex make a regular hexagon.
A strange and interested thing about this solid using PP bands is that we can look it as other type of ”semi – regular polyhedron”.
Please look at figure 2. We write lines on the central part of the PP bands. Then you get that this solid is also a ”semi – regular polyhedron” made of regular pentagon and regular triangles. We call it a “Icosidodecahedron”.
There is a little defference between truncated icosahedron (figure 1) and icosidodecahedron (figure 2).
A truncated icosahedron has 2 types of the sides. One type (blue lines) are sandwiched between a regular pentagon and regular hexagon and another type (green lines) are sandwiched 2 regular hexagon. On the other hand, all sides (yellow lines) of icosidodecahedron are sandwiched between a regular pentagon and regular triangle. Then icosidodecahedron are distinguished from other semi – regular polyhedron and called “quasi – regular polyhedron”.
by Tsuyoshi Sonoda (Math Dept.)

今日5月9日を3ケタの数で表すと、509は素数です。西暦を含めた20190509は、17×53×22409と素因数分解できるので、素数ではありません。

今、サッカーボールのデザインはさまざまなものがありますが、その中でも昔からある正五角形と正六角形でできた白黒のデザインは誰でも思い浮かぶのではないでしょうか。下の3つのサッカーボールのうち、右の2つは正五角形と正六角形でできていますね。

数学の世界では、2種類の正多角形からできている立体を「半正多面体」と言い、サッカーボールには、「切頂（せっちょう）二十面体」や「角切り（かくぎり）二十面体」という名前がついています。この名前はこの立体の作り方から来ています。写真1の白い立体は正二十面体です。正二十面体には12個の頂点があります。この頂点を写真2のように切り取っていくと、あっという間にサッカーボールが現れました。

このお話を読んだ皆さんは、もし「サッカーボールの正五角形と正六角形は何枚ずつあるの？」と聞かれることがあれば、正解を答えられますよね。
そうです。正二十面体の12個の頂点を切り取ってできた正五角形は12枚、正二十面体の元の面からできている正六角形はもちろん20枚ですね！
（数学科 園田毅）

“A soccer ball is a famous solid!”
There are many designs with soccer balls now. Among them, many people know the design with black pentagons and white hexagons.
In the mathematics world, we call them “semi – regular polyhedron”, that include multiple regular polygons like a soccer ball. A soccer ball is a solid ‘Truncated icosahedron’ in English, ‘Settyo nijumentai’ or ‘Kakugiri nijumentai’ in Japanese. The name of this solid, both in Japanese and English, means a way of making this solid. The white solid in figure 1 is a regular icosahedron. A regular icosahedron has 12 vertex. We cut those vertex as in figure 2, so we can get a soccer ball instantly.
Those who have read this blog can answer the question ‘How many numbers of regular pentagons and regular hexagons are in a truncated icosahedron?’
Yes, numbers of regular pentagons are 12 pieces in a truncated icosahedron because a regular icosahedron has 12 vertex. And numbers of regular hexagons are 20 pieces because those are the same as the numbers of original faces of regular icosahedron.
by Tsuyoshi Sonoda (Math Dept.)

今日4月21日を3ケタの数で表すと、421は素数です。西暦を含めた20190421も素数になります。

今回作ったシェルピンスキー四面体の体積は元の正四面体4つ分で、シェルピンスキー四面体と同じ大きさの正四面体の体積は元の正四面体8つ分なので、体積比は1：2であることを紹介しました。
シェルピンスキー四面体は正四面体の内部に穴が開いた立体なのですが、前回のブログで、内部の形がどうなっているか皆さんに質問をしました。実は、同じ折り紙ユニットで作った正八面体がぴったり入るのです。つまり、正八面体の体積は同じ辺の長さの正四面体4つ分であることがわかります。
私たちは、小さな正四面体を合体してシェルピンスキー四面体を作りましたが、実際のシェルピンスキー四面体は正四面体の内側に連続して穴を開けてできるイメージです。左の写真は本校の近くにある京都大学総合博物館に展示されているシェルピンスキー四面体の模型です。
また、京都大学「シェルピンスキーの森」（写真下）をはじめ、日本各地にこの図形を利用した日よけが設置されています。（ららぽーと豊洲、東名阪自動車道御在所サービスエリアなど）太陽の光がこの図形を通ると、木漏れ日のある光景が現れ、暑さが和らぐそうです。「フラクタル日よけ」と呼んでいます。海外では2019年1月にオープンした台湾・台南市美術館2号館（日本の建築家 坂茂氏が設計）に、フラクタル日よけの屋根が採用されているそうです。
シェルピンスキー四面体は、とても不思議でおもしろい図形ですね。ぜひ数学博物館の展示もご覧になってください。
（数学科　園田）

“Sierpinski tetrahedron 2”
In the last blog, we said that the volume of a Sierpinski tetrahedron is 4 times of an original regular tetrahedron and a ’big regular tetrahedron’ is 8 times of an original regular tetrahedron, then the ratio is 1:2.
I also had a question for you in the last blog. What form is the space in a Sierpinski tetrahedron ? The answer is a regular octahedron by the same origami units fits perfectly. We can get that a regular octahedron is 4 times as a small regular tetrahedron.
This time, we united with small regular tetrahedron and made a big Sierpinski tetrahedron. In fact, please imagine that you make holes in a regular tetrahedron continuously. This is a model of Sierpinski tetrahedron exhibited in Kyoto University in the right photo.
There are some sunshades using this figure in Japan, for example, ‘The forest of Sierpinski’ in Kyoto University near our school, the shopping area ‘LaLaport TOYOSU’ in Tokyo and Gozaisho Service Area on Higashimeihan Expressway in Mie prefecture, etc. After the light of sun goes through this sunshade, we can see the scene with filtered sunlight and the heat getting let up. It is called a ‘fractal sunshade’. Tainan Art Museum opened in January 2019, building No.2 adopted the roof of fractal sunshade overseas.
Sierpinski tetrahedron is a mysterious and interesting shape. Please check the exhibit in our Museum!
by Tsuyoshi Sonoda (Math Dept.)

今日、3月11日を3ケタの数で表すと、311は素数です。西暦を含めた20190311は、173×116707と素因数分解できるので、素数ではありません。

中学1年生は立体の授業で正多面体を学習します。正四面体と正八面体、正二十面体は同じ折り紙ユニット（正四面体は2枚、正八面体は4枚、正二十面体は10枚）で作って、実際に面、辺、頂点の数を数え、構造を確認しています。左の写真は折り紙ユニット（左右逆に折ることで、「正折り」と「逆折り」を区別することが必要です）、右の写真は完成した正四面体と正八面体です。

今回は、この正四面体を4つ合体させて作った「シェルピンスキー四面体」をご紹介します。正四面体がシェルピンスキー四面体の各頂点の位置に置かれ、シェルピンスキー四面体の一辺の長さは、元の正四面体の2倍になっています。
シェルピンスキー四面体と同じ大きさの正四面体と表面積、体積を比べてみましょう。シェルピンスキー四面体の内部に入った元の正四面体の面がシェルピンスキー四面体の「穴」を埋めることになり、2つの立体の表面積は変わりません。
次に体積を比較してみましょう。シェルピンスキー四面体の体積は元の正四面体4つ分で、正四面体の体積は元の正四面体8つ分（相似比1：2から体積比は1：8とわかります）なので、体積比は4：8＝1：2となりますね。
最後に質問です。今回作ったシェルピンスキー四面体内部の空間は、どんな形になっているでしょうか。実際に作るか、頭の中で考えてみてください。
（数学科　園田）

“Sierpinski tetrahedron 1”
Our students study regular tetrahedron in the unit of solids in 9th grade. We make tetrahedron, octahedron and icosahedron by the same origami unit. After that, we count the number of faces, edges and vertex and study the structure of those. I show the origami unit in the right picture and a tetrahedron and a octahedron in the left picture below.
We will introduce Sierpinski tetrahedron gathering 4 regular tetrahedron. 4 regular tetrahedron are placed at each vertex of Sierpinski tetrahedron and the length of each side of Sierpinski tetrahedron is twice the length of each regular tetrahedron.
Let’s compare the Surface area and Volume of Sierpinski tetrahedron with ’big regular tetrahedron’ which has same length as the Sierpinski tetrahedron. Faces of regular tetrahedron in a Sierpinski tetrahedron overlap the hall of a Sierpinski tetrahedron.
2 solids have the same surface area.
Next, let’s compare the volume. The volume of a Sierpinski tetrahedron is 4 times of an original regular tetrahedron and ’big regular tetrahedron’ is 8 times of an original regular tetrahedron (the volume ratio is 1:8 because similarity ratio is 1:2), then the volume ratio is 4:8=1:2.
Finally, I have a question for you. What form is the space in a Sierpinski tetrahedron? Find the answer by making or thinking.
by Tsuyoshi Sonoda (Math Dept.)

本日2月27日を3ケタの数で表した227は素数です。西暦を含めた20190227も素数になります。

前回、正多面体はたった５種類、正四面体、正六面体（立方体）、正八面体、正十二面体、正二十面体しかないことを紹介しました。今日は、その解答編です。

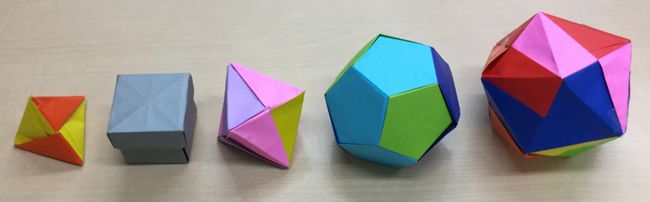
ポイントは2つです。1つ目は、正多角形が3枚以上でないと立体の角（かど）を作ることはできません。もう1つは、角に集まる正多角形の角度の合計は360度未満でなければなりません。
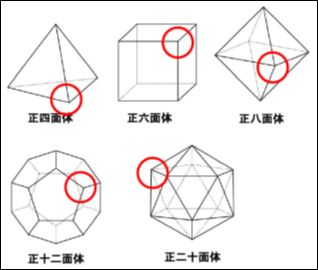まず、正六角形で正多面体を作ることは不可能です。正六角形の１つの内角は120度なので、１つの頂点に正六角形が３枚集まるとその角度の和は360度となり、角が平らになって正多面体を作ることはできません。そうです。角に集まる正多角形の角度の和が360度より小さくならないと、尖った角ができないのです。
次に、正三角形、正方形、正五角形の場合を考えてみましょう。
１つの頂点に正三角形が３枚ずつ集まると正四面体、４枚ずつ集まると正八面体、５枚ずつ集まると正二十面体ができます。が、正三角形６枚の角度の和は360度なので、これ以上の枚数の正三角形で正多面体を作ることはできません。
１つの頂点に正方形が３枚ずつ集まると正六面体ができますが、正方形の１つの内角は90度なので、正方形４枚の角度の和は360度なので、これ以上の枚数の正方形で正多面体を作ることはできません。
１つの頂点に正五角形が３枚ずつ集まると正十二面体ができますが、正五角形の１つの内角は１０８度なので、正五角形４枚の角度の和は360度以上となり、これ以上の枚数の正五角形で正多面体を作ることはできません。
これが、正多面体が５種類しかない理由です。
（数学科　園田）

“Only 5 kinds of Regular polyhedron! 2”
I talked about how there are only 5 kinds of regular polyhedron, tetrahedron, cube, octahedron, dodecahedron and icosahedron in the last blog. I will show the reason this time.
There are 2 points. One is that we can make verities by more than 3 polygons. The other is that the sum of angles of regular polygons gathering at a point are less than 360 degrees.
First, it is impossible to make a regular polyhedron by regular hexagons. An interior angle of a regular hexagon is 120 degrees. The sum of the angles of 3 regular hexagons gathering at a point are 360 degrees. So 3 regular hexagons can’t make a vertex because those get to be flat.
You know that we can make a corner where the sum of angles are less than 360 degrees.
Next, we think about triangles, squares, pentagons. We can make tetrahedron by 3 regular triangles, octahedron by 4 regular triangles, icosahedron by 5 regular triangles gathering at a point. But the sum of the angles of 6 regular triangles are 360 degrees, so we can’t make polyhedron with more than 6 regular triangles.
We can make cube by 3 squares gathering at a point, but the sum of the angles of 4 squares are 360 degrees , so we can’t make polyhedron with more than 4 squares.
We can make a dodecahedron by 3 regular pentagons gathering at a point, but the sum of the angles of 4 regular pentagons are over 360 degrees, so we can’t make polyhedron with more than 4 regular pentagons.
This is why there are only 5 kinds of regular polyhedron.
by Tsuyoshi Sonoda (Math Dept.)