Do★Math 数学博物館 Mathematics Museum
数学科メディアスペースにある、数学だけの博物館では、昔使われていた携帯そろばんや鯨尺ものさし、ピタゴラスの定理パズルや展開・因数分解パズルなど、数学にまつわるさまざまなものを展示をしています。
「Do★Math 数学博物館」からのお知らせ
私たちは、算数・数学を手に触れたり、パズルやゲームでわかりやすく、そして楽しみながら理解できる「Do★Math 同志社中学校数学博物館」を2016年5月にオープンいたしました。展示物の多くを並べた数学科オープンスペース（「数学メディアスペース」）を中心に、数学教室ゾーンを総称して、Do★Mathです。
このページでは、ブログでDo★Mathの展示物を皆さんに紹介していきます。展示内容を知っていただくとともに、数学読み物としても楽しめる連載にしていきたいと考えています。
発行は月2回不定期に、月日を合わせた3ないし4ケタの数字が素数の日に発信します。例えば、5月23日は523と表すことになり、523は素数です。
★3種類まとめて購入すると、送料無料！（2020年9月より当面の間）
ユーレカ・キューブ ～“Eureka Cube”
2月11日を3ケタの数で表した211は素数です。西暦を含めた20240211は、3×6746737と2つの素数の積で表されるので素数ではありません。
最近、ユーレカ・キューブ（ユーレカのキューブ）を知りました。
8つのピースから、1辺の長さが3、4、5となる立方体を作り、さらに組み直して1辺が6の立方体を作ることができます。
33＋43＋53 ＝ 63 （＝ 216）
となることを示しています。通信販売で購入した2cm角の木製立方体を接着してピースを作り、着色して完成しました。
1辺3の立方体（左下）はこれだけで1ピース、1辺4の立方体は写真下の2つのピースでできます。残り5つのピースで1辺5の立方体を作るのが難しいです。もし、1色に塗っていたら難度は跳ね上がると思います。
この3つの立方体を8ピースに戻し、組み立て直すと、1辺6の立方体が出来上がります。
これも作るのは難しいです。私は最後に写真右上にある1辺4の立方体から2つ欠けているマリンブルーのピースをはめ込んで完成しましたが、欠けている部分のはまり方に感動しました。
ユーレカ・キューブは、以前は販売されていたようですが「品切れ」となっていたりして、今販売しているサイトを見つけることはできませんでした。ネット販売やホームセンターで木片を購入して自作するのが手軽だと思います。
高木茂男「Play puzzle パズルの百科」（1981初版 平凡社 p70）に「ユーレカのキューブ」が紹介されています。イギリスにあるケンブリッジ大学数学協会が発行するジャーナル「Eureka」（ユーレカ）に紹介されたのが初めてと記されていました。ちなみに、ケンブリッジ大学（University of Cambridge）はニュートンやダーウィンも学んだ大学です。
この本では、8個に分割されているピースが紹介されていますが、ユーレカ・キューブについて書かれている記事を調べると、直方体9ピースでできている分割方法も紹介されていました。
直方体ピースのユーレカ・キューブも作る予定でいます。
ぜひ博物館におこしになって、チャレンジしてみてください。
（数学科 園田毅）
“Eureka Cube”
I recently learned about the Eureka Cube.
From the 8 pieces, we can create cubes with side lengths of 3, 4, and 5 blocks, and then reassemble them to create cubes with a side length of 6 blocks.
You can make a cube.
Expressed numerically, it looks like this.
33＋43＋53 ＝ 63 （＝ 216）
Each block was made with a 2cm square wooden cube, then finished by coloring.
The “Eureka Cube” is introduced in Shigeo Takagi’s “Play Puzzle Encyclopedia” (1981 first edition Heibonsha p70-71).
A piece divided into 8 pieces is introduced. When I looked up an article written about the Eureka Cube, I found that it also introduced how to divide a rectangular parallelepiped into 9 pieces.
A cube with a side length of 3 blocksis just one piece. The 4 cube is easy tomake as there are only two pieces.
I think a cube with sides of 5 blocks or6 blocks is quite difficult.
Please come to the museum and giveit a try.
by Tsuyoshi Sonoda (Math Dept.)
数学博物館見学会を開催しました
9/16土午前、Do★MATH同志社中学校見学会を開催しました。
10組の小学生・ご家族様がご参加くださり、博物館の見学、折り紙、「ミウラ折り」を一緒に楽しみました。
今回のメイン体験は、宇宙空間での応用が進められているミウラ折りです。折りたたみ地図を作って、ミウラ折りの便利な性質を体験しました。普通に紙を折ると折り目が長方形になりますが、「ミウラ折り」は折り目が平行四辺形を作るように折ります。この発明で、宇宙飛行士が船外活動することなく太陽光パネル等の組み立て作業をできるようになっています。（宇宙実験・観測フリーフライヤ SFU等）
参加者の皆さんの学びを楽しむ様子がすばらしかったです！
ご来館くださった皆さま、ありがとうございました。
（数学科 園田）
牛乳パックでシェルピンスキー四面体
“Sierpinski tetrahedron by milk cartons”
4月21日を3ケタの数で表すと、421は素数です。西暦を含めた20200421は、3581×5641と2つの素数の積で表されるので素数ではありません。
2019年度中学3年生は、ピタゴラスの定理の応用で、牛乳パックで正四面体と正八面体を作り、その体積を計算しました。
1Lの牛乳パックを約半分(高さ約12 cm)に切ったパーツ1つで一辺14 cmの正四面体1つ、パーツ2つで正八面体を1つ作りました。（写真2&3） これらの体積をピタゴラスの定理を使って計算すると、意外な結果が出るところもおもしろいです。興味のある方はぜひ体積を計算してみてください。その後、1人が1つ作った正四面体を合体させて、学年で1つのシェルピンスキー四面体を製作していきました。（写真1）
これが256個、16段に重なって、180 cmを超える（11.4×16＝182.4 cm）シェルピンスキー四面体ができあがりました。春休み中、数学1教室「ピタゴラス」で展示しました。
（写真4＆5）は、64個による大きなシェルピンスキーの山が3つできたところです。
4個の山（2段の正四面体）をシェルピンスキー四面体1ユニットとすると、牛乳パック4個の容積と中空部分の体積は同じです。しかし、4ユニット（16個4段）、16ユニット（64個8段）、64ユニット（256個16段）になるにつれて、牛乳パックが占める容積は完成されたシェルピンスキー四面体の4分の1、8分の1、16分の1になってしまいます。
このように、シェルピンスキー四面体はとても不思議な立体です。興味を持ってくださったらうれしいです。
（ 数学科 園田毅）
“Sierpinski tetrahedron by milk cartons”
Our 9th grade students made regular tetrahedron and octahedron with milk cartons, and calculated their volume using Pythagorean’s theory.
Our students made a regular tetrahedron, 14 cm on a side with a piece that is a part cut about half of a milk carton, and a regular octahedron the same length on a side in 2 pieces. (Figure2&3) It is interesting that will be a wonderful result when you calculate these volumes of 2 solids. Let’s try to calculate if you are interested in these things. Then we made a big Sierpinsky tetrahedron gathering regular tetrahedron, where 1 student made 1 regular tetrahedron. (Figure1)
We made a big Sierpinski tetrahedron with 256 pieces, 16 tiers and more than 180 cm. We exhibited it in math classroom 1 “Pythagoras” during spring vacation.
There are 3 masses of Sierpinski tetrahedron with 64 regular tetrahedron in figure 4 & 5.
If we define Sierpinski tetrahedron with 4 regular tetrahedron as 1 unit, the volume of 4 pieces of milk cartons and the space of 1 unit of Sierupinski tetrahedron are same. But when Sierpinski tetrahedron become 4 units (16 pieces, 4 tiers), 16 units (64 pieces, 8 tiers), 64 units (256 pieces, 16 tiers), the volume of the milk cartons gets smaller by a 1/4, 1/8, 1/16.
This is why that Sierpinski tetrahedron is a mysterious solid. We would be happy if you got interested in it.
by Tsuyoshi Sonoda (Math Dept.)
2進法時計（バイナリークロック）
～“The binary clock”～
今日4月9日を3ケタの数で表すと、409は素数です。西暦を含めた20200409は、37と419、1303の3つの素数の積で表されますので素数ではありません。
今回は、2進法表示の時計（バイナリークロック）を紹介します。通信販売で購入しました。
見た目はヨーロッパの建物ですが、実は窓の灯りで時間を表示するおしゃれでユニークな時計です。内部は空洞で、ICチップとLEDランプが接続されています。
時間の表示方法が変わっています。
窓のタテ4列は左から「何時」の十の位、一の位、「何分」の十の位、一の位を表しています。一方、1階は「1」、2階は「2」、3階は「4」、4階は「8」を表します。写真2では19時29分、写真３では4時17分を示しています。1つも窓が灯ってない列は0を意味しています。正確には2進法的な表示です。慣れたら、小学生の皆さんも読めると思います。写真を見て、チャレンジしてみてください。「1」、「2」、「4」、「8」のあるなしで、0ー9を表せることを確かめてみてください。
この時計は数学博物館に展示してありますので、ぜひ楽しんでください。最大1分間、時計を見つめてくださったら、光の「針」が動きます。
（ 数学科 園田毅）
“The binary clock”
We will introduce the binary clock. We bought it on the internet.
It looks like a European building, but it is a cool and unique clock. There is a space in the clock, with only an IC chip and LED lamps in it.
The way to show the time is strange. The vertical lines of windows indicate, from the left to right, ten’s place and one’s place of “hours” and ten’s place and one’s place of “minutes”. On the other hand, the horizontal lines of windows indicate that the first floor means “1”, the second floor means “2”, the third floor means “4” and the forth floor means “8”. The clock in figure 2 indicates 19 hours 29 minutes and figure 3 indicates 4 hours 17 minutes. The line where no lights are on means 0. This clock uses the way like a binary system exactly. Maybe elementary school students can read the time of this clock. Let’s try looking at the figures. Please make sure we can show the numbers from 0 to 9 using or not using “1”, “2”, “4” and “8”.
We exhibit this clock in our math museum, so please enjoy it! The “clock hands” of the light will move if you look at the clock for more than one minute.
by Tsuyoshi Sonoda (Math Dept.)
フィボナッチ数列板
～ “Fibonacci numbers board” ～
今日2月11日を3ケタの数で表すと、211は素数です。西暦を含めた20200211は、 19×29×61×60131と素因数分解できるので素数ではありません。
数学エリア3階の本棚の上に、「フィボナッチ数」が書かれた板を設置してあります。フィボナッチ数（数列）は、
1、1、2、3、5、8、13、21、34、55 ･･･
と数が続いていきます。直前の2つの項をたすと、次の項になるというしくみです。
フィボナッチ（1170頃ー1250頃）は、彼の著書「算盤の書」（1202）の中で「ウサギの問題」としてこの数たちを紹介しました。次のような内容です。
＜ウサギのつがい（組）の増え方＞
（１）1組のウサギは産まれて1ヶ月で大人になり、2ヶ月後から1組のウサギを産む。
（２）ウサギは死なない。
スタートは赤ちゃんウサギ1組です。1ヶ月後は大人ウサギ1組になり、2ヶ月後は大人ウサギ1組と赤ちゃんウサギ1組で計2組、3ヶ月後は大人ウサギ2組と赤ちゃんウサギ1組で計3組、4ヶ月後は大人ウサギ3組と赤ちゃんウサギ2組で計5組…というふうに増えていきます。
また、フィボナッチ数は自然の中に実際に存在していることで有名です。ひまわりや松ぼっくり、パイナップルの螺旋の数、多くの花びらの枚数がフィボナッチ数になっています。
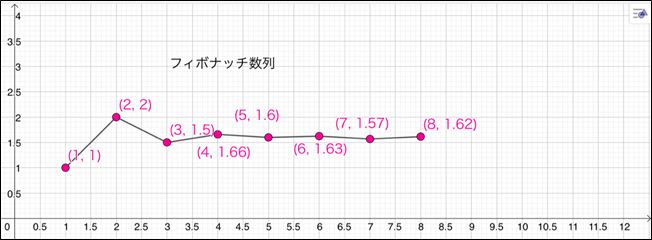
さらに、フィボナッチ数にはおもしろい性質があります。1つの数をその手前の数で割ると、 だんだん「黄金比＝1.618 ･･･ 」と表される数に近づいていくのです。最初は1/1＝1からスタートしますが、3/2＝1.5、 5/3＝1.666 ･･･ 、 8/5＝1.6、 13/8＝1.625と進み、あっという間に1.618 ･･･ に近くなっていきます。
フィボナッチ数の魅力をいくつか紹介しました。興味を持ってくださった方はぜひ調べてみてください。
（数学科 園田毅）
下のグラフは、1つのフィボナッチ数をその手前の数で割ると、だんだん「黄金比＝1.618 ･･･ 」と表される数に近づいていく様子をGeoGebraで描いたものです。ｙ座標がだんだん1.618 ･･･ に近づいていきます。
GeoGebraは、幾何、代数、解析を1つに結びつけた動的数学ソフトウェアです。
参考URL: https://sites.google.com/site/geogebrajp/
ジョセフ・ダグニーズ著、ジョン・オブライエン画
「フィボナッチー自然の中にかくれた数を見つけた人」
2010 さえら書房
三浦伸夫著
「フィボナッチ アラビア数学から西洋中世数学へ」
2016 現代数学社
“Fibonacci numbers board”
We put the board with “Fibonacci numbers” written on it on the bookshelf on the third floor in our math area.
Fibonacci numbers (sequence) are below.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ･･･
The previous 2 numbers make the present number. For example,
1＋1 ＝ 2、5＋8 ＝ 13、21＋34 ＝ 55 etc.
Fibonacci introduced these numbers as the problem with rabbits in his book ‘Liber Abaci’ (1202). The contents are as follows.
Way of increasing rabbit pairs
(1) A pair of rabbit become an adult 1 month after their birth and have a pair of babies.
(2) Rabbits never die.
First, there is 1 pair of baby rabbits. They become 1 adult pair 1 month after birth, become 2 pairs including 1 adult pair and 1 baby pair 2 months after, become 3 pairs including 2 adult pairs and 1 baby pair 3 months after, and become 5 pairs including 3 adult pairs and 2 baby pairs 4 months after.
Also, Fibonacci numbers are famous for its presence in nature. The numbers of spiral in a sunflower, a pine corn and a pineapple, and the numbers of many kinds of flower petals are Fibonacci numbers.
Besides, there are interesting characteristics in Fibonacci numbers. The answer of the value what a Fibonacci number divided by the second number
gets close to the golden ratio. 3/2 ＝ 1.5, 5/3 ＝ 1.666 ･･･ ,
8/5 ＝ 1.6, 13/8 ＝ 1.625, it is getting close to 1.618･･･ in this way.
We introduced the fascination of Fibonacci numbers. Let’s research them if you take an interest in them.
by Tsuyoshi Sonoda (Math Dept.)
