Do★Math 数学博物館 Mathematics Museum

本日10月21日を1021と4ケタの数で表すと、1021は素数です。なんと、西暦を含めた20161021も素数です！

毎年3月、中学3年生が問題と解答を作成し、それを記入した算額（絵馬）が「同志社中学校算額展」として三井寺（みいでら　滋賀県大津市）に掲示、紹介されています。三井寺は比叡山の山麓にあり、関西の桜の名所としても有名なお寺です。観音堂には江戸時代の「算額」が飾られていて、目の前で見ることができます。
江戸時代に発達した日本独特の数学を「和算」と言います。武士階級だけではなく、農民も和算を学びました。彼らは年貢を計算して庄屋や代官と交渉しました。江戸時代のベストセラーと言われる庶民向け数学書「塵劫記（じんこうき）」を著した吉田光由（よしだみつよし　1598-1673）、「点竄術（てんざんじゅつ）」を発明した関孝和（せきたかかず1642-1708）、円周率を41ケタまで計算した建部賢弘（たけべかたひろ　1664-1739）など、この時代には世界に誇るべき数学者がいました。
また江戸時代には、数学の問題を書いた「算額」を寺社に奉納する風習があり、近畿では三井寺をはじめ、北野天満宮、八坂神社、清水寺などの寺社に現存しています。
生徒が作成した絵馬には、表面に問題、裏面に解答と作成者の名前が入っています。3年生の作った絵馬は、1年間、三井寺釈迦堂に展示された後、数学ＭＳおよび廊下に展示しています。

“Do you know Sangaku ?”
“Sangaku” (votive tablet depicting a math puzzle) written by our students are exhibited at Mii-dera Temple, from March each year. They made math problems and solutions and wrote them on the board “Sangaku”. Mii-dera Temple is located at the foot of Mt.Hiei.
“Wasan” is Japanese original mathematics developed in the Edo period. I’ll introduce three mathematicians. Yoshida Mitsuyoshi(1598-1673) published “Jinkoki” which is an introductory book of math for the people in the Edo period, Seki Takakazu(1642-1708) invented “Tenzanjutu”, the way of solution of an equation. Takebe Katahiro(1664-1739) calculated pi [π] to 41-digits.
There were customs where people dedicated “Sangaku” in the Edo period. Now we can see them at Mii-dera Temple, Kitano Tenmangu Shrine, Yasaka-jinja Shrine and Kiyomizu-dera Temple.

本日10月13日を1013と4ケタの数で表すと、1013は素数です。なんと、西暦を含めた20161013も素数です！

１＋２＋３＋・・・＋１４＋１５ は？

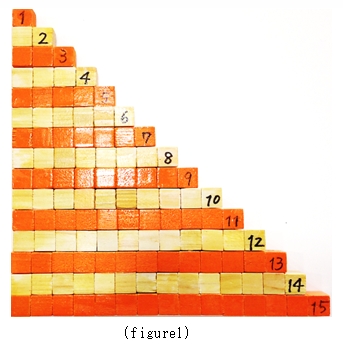
ひとつずつ順に計算していくとたいへんですね。右の階段状の立体(写真1)は、上の式のモデルです。各行の立方体の個数がその行の右端に書いてあります。
だから、階段状の板は、
１＋２＋３＋…＋１３＋１４＋１５（個）

の合計を表しています。
このまま、順にたしていくのはたいへんなので、同じ板を２枚合体させてみましょう。(写真2)
タテが１５ｃｍ、ヨコが１６ｃｍの長方形になりますね。だから、答えは、

１５×１６÷２ ＝ １２０（個）

とな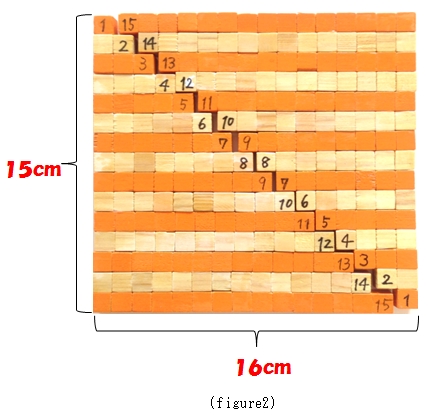ります！ 確かめてみましょう。
数学者ガウス（ドイツ 1777－1855）は、小学生のとき、１から１００までの数の合計を求める課題を出されたのですが、彼がどのように解いたか、皆さんもうおわかりですね。

１００×（１００＋１）÷２ ＝ ５０５０

“What is the sum of natural numbers?”
１＋２＋３＋・・・＋１４＋１５＝？

It is difficult to calculate one by one.

There is a solid like some stairs. It is a model of the above expression. (figure1)The number on the right side shows the quantum of the small cubes each row.
So this board means the sum of

１＋２＋３＋・・・＋１４＋１５＝？

Now we unite 2 solids into 1 and we can see a rectangle. (figure2)
The vertical length of this rectangle is 15, the horizontal length is 16.

So the answer is
15×16/2=120

There is famous story about the calculation above.
When a mathematician, Gauss (Germany 1777-1855), was an elementary school student, his teacher asked his students to get the sum of natural number from 1 to 100. He soon solved the problem.
You can see his way of solving.

100×(100＋1)/2=5050

本日9月29日を929と3ケタの数で表すと、929は素数です。西暦を含めた20160929は17と69761で割り切れるので、素数ではありません。皆さんも計算してみてください。

１＋２²＋３²＋…＋○²
と続く、自然数の２乗の合計はいくつになるのか考えてみましょう。
実は公式があります。１から○までの自然数の２乗の合計は次のような形にまとまります。高校生、大人の方は、○の部分をｋやｎで学習した記憶があるのではないでしょうか。
１²＋２²＋３²＋…＋○²
＝１＋４＋９＋…＋○²

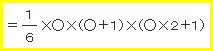
この公式を具体的に立方体の個数として表したのが、この模型です。（写真1）白の立方体が1個、黄が4個、水色が9個、青が16個、橙が25個となっています。この模型は、５² までの合計のモデルにしたので、➄という数字に注目してください。

この模型を３セット合体すると、写真2のようになります。
がんばって、６セット合体してみてください。写真3のような直方体になります。
このとき、全ての立方体の個数を直方体の体積として考えることができますね。

➄を○に直すと、公式ができますね。

“What is the sum of natural numbers squared?”
Let’s talk about the sum of natural numbers squared.
There is a formula.
１²＋２²＋３²＋…＋○²
＝１＋４＋９＋…＋○²

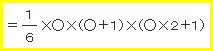
This model is specifically indicating the formula as numbers of small cubes.
There are 1 piece of white cube, 4 pieces of yellow, 9 pieces of light blue, 16 pieces of blue and 25 pieces of orange.
Please check the number 5 in case of n=5 on this model.
First, we combine 3 sets of this model into 1 solid, as we can see in figure2.
Second, we combine 6 sets of this model into 1, so we can see a rectangular parallelepiped in figure3.
So we can see the length of the rectangular parallelepiped in figure3.

When we change 5 into n, we can get the formula!

本日9月7日を907と3ケタの数で表すと、907は素数です。西暦を含めた20160907は13、281、5519で割り切れるので、素数ではありません。皆さんも計算してみてください。

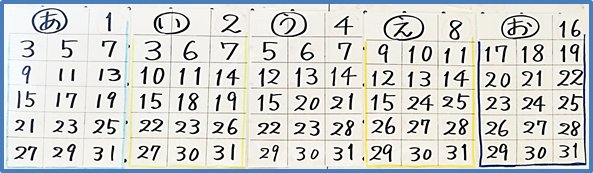
来館くださった子どもたちに人気なのが、誕生日当てゲームです。数字の書かれた5枚のカード（あ）から（お）があり、そこには1から31までの中で16個ずつ数字が書かれています。そして、子どもたちから自分の生まれた日付のあるカードを教えてもらうだけで、誕生日を当てることができるのです。
種明かしをしましょう。それぞれのカードの右上には、（あ）から順に1、2、4、8、16と書いてあり、日付のあるカードの右上の数字を足せば生まれた日付になります。コンピュータで使われている2進法を応用したゲームですが、その原理を中学1年生で学んでいます。

“A game to guess the right birthday”
We will introduce a game to guess the right birthday. It is popular for young visitors in our exhibition. There are five cards (a), (i), (u), (e), (o) in Japanese characters. Each card shows 16 numbers from 1 to 31.
First, a customer chooses the cards that show one’s birthday in five cards.
Next, we check the number ‘1’, ‘2’,’4′, ‘8’ and ’16’ in upper right on the cards that the customer choice. We add the numbers and get one’s birthday.
This is a game that applies the binary number system used by computers. Our 7th grade students study its principle.

本日8月23日を823と3ケタの数で表すと、823は素数です。西暦を含めた20160823は13、89、139で割り切れるので素数ではありません！

弘中又市さん（1873-1938）は、1912年から1932年まで同志社中学校で数学の教員をしていたのですが、以前、松山中学校で働いたことがありました。（1895-1896） そして、そこには、当時、英語の教員だった夏目漱石がいたのです。そうです。弘中又一さんは夏目漱石が書いた「坊ちゃん」のモデルだったのです。
彼の肖像画と資料が本校3階数学MSに展示してあります。

“Do you know Hironaka Mataichi?”
He worked as a math teacher at our school from 1912 until 1923. Before his career at our school, he worked at Matsuyama Junior High School from 1895 until 1896.
Natsume Soseki, who is a famous Japanese writer, also worked there. So, Hironaka Mataichi is a model of ‘Botchan’, that is a novel of Natsume Soseki.
We have his portrait and other data about him on the third floor in our math space.