＜英語で数学_解決編＞「不思議の国のアリス」で数学しよう（図形＆傾き）

皆さんは「TED」（TED talks）をご存じでしょうか。さまざまな分野の方が行う、英語のプレゼンテーションスピーチを配信する動画配信サービスです。そのサービスの一つに、教育向け動画「TED-Ed」があります。Edは教育（Education）の略です。算数・数学に関しても楽しく学べる動画が数多くあります。今回は、その中の「The Alice in wonderland riddle？」を活用した授業をご紹介します。
図形の傾きがテーマですので、「平面図形」、「比例・１次関数」、「相似な図形」などの単元の教材に適しています。今回は、１年生２学期最初の授業、いわゆる「授業開き」で実施した２回分の後半です。

（１）いじわるな女王がAliceに出した謎（riddle）
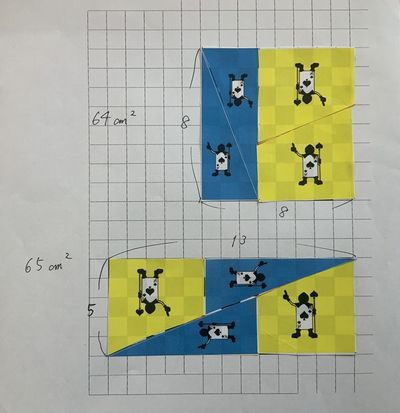
「64は65と等しい」と言いはります。さらに「トランプの兵士」に命じて、その「証明」をします。
右の図では、8×8＝面積64と面積65の格子に、同じ4つの「トランプの兵士」がぴったりはまって「64」＝と「65」になっているように見えます。
が、これが女王のトリックなのです。
解けなければ、Aliceは死刑になってしまいます。
皆さんにはぜひいじわる女王のトリックを見破ってAliceを救い出してほしい、という設定です。

（２）この動画の後半には謎解きもあるのですが、前半の問題編で一旦映像をストップして、女王がアリスに提示したことを実際に体験してみます。
トランプの兵士たち（青と黄色のピース）を印刷した用紙を配って切り貼りしました。同じことをロイロノート上でも図形を動かして確認しました。

（３）グループで気づいたことを話しあう
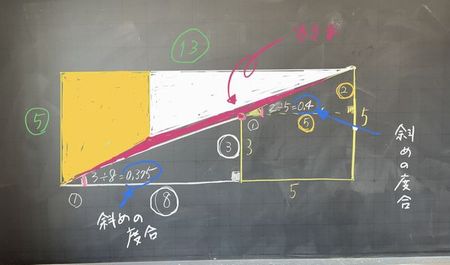
話し合っている様子を聞くと、「斜めのところにすき間がある」とか「まっすぐじゃない」などの声も聞こえてきました。
解決への第一歩として、面積65の長方形の対角線近辺にすき間があって、そこに面積が1増えた秘密がありそうだということを確認しました。
2、3年生でしたら比例・１次関数でグラフの「傾き」や「相似な図形」を学習していますので、その知識を使って数値を使った説明になります。模範的な解答は次のようなものになります。

が、１年生は「傾き」を正式には学習していないので、今各自が持っている知識を使って、説明を作り出すことになります。
2回目の授業のテーマは「なぜ対角線のところにすきまができるのか」です。このことを数字を使って、説明できるようになるのがこの授業も目標になります。グループでも話し合いながら考えてもらいました。

（４）「相似」、「面積」、「傾き」による説明
説明できるという方にロイロノートの画面を共有して説明してもらいました。「タテとヨコの比が違うから相似な三角形でない」、「長方形の対角線に見えているところは直線でない」といった表現でしっかり解説をされました。

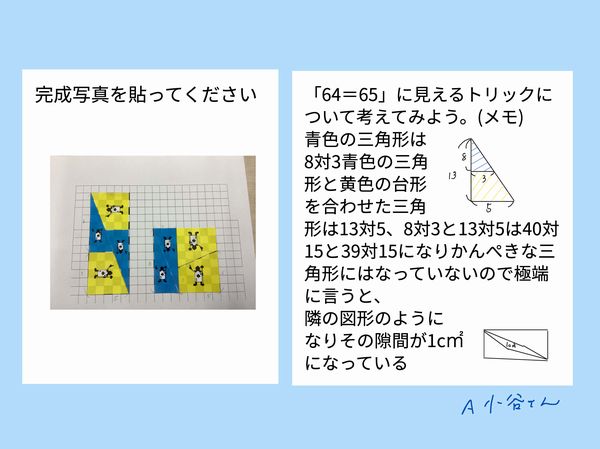
お2人の説明をご紹介します。最初の方は青い三角形と、長方形の対角線で仕切られる三角形の「傾き」が違うことを「相似」を使って説明されました。次の方は、青い三角形と黄色い台形の面積の合計が64なので、対角線がまっすぐではない（そこにすき間がある）という結論を導いてくださいました。今持っている知識を使って、問題を考える姿勢がすばらしいと思いました。

（５）これから、図形や角度について深く学習していきますし。また、「傾き」は比例・1次関数といった直線グラフで直接学習します。今回のような「傾き」を活用する問題（それを活用するというヒントはない問題）に接したときに、斜めの度合いを数値化して表せる「傾き」、「tanθ」のありがたさを感じてもらえるとうれしいと思います。

※付録1
台形と三角形のピースは、PowerPointの「図形」「フリーフォーム」で作りました。
長方形の余白は透明になっている。または、「背景削除」でも可能。
タブレットのSplit View機能でロイロノートとPowerPointを開き、PowerPoint上の図形をロイロノートにスワイプ（移動）すると、そのままコピーされる。（ロイロノートとkeynoteは不可）

※付録2
◎動画に出てくる数学用語を英語でご紹介します。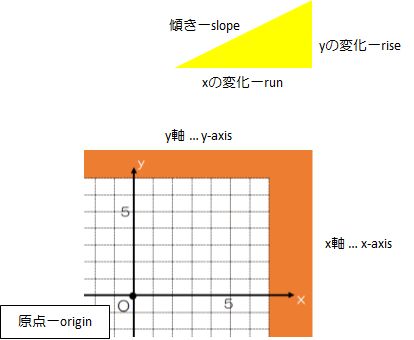
関数ーfunction
正比例ーproportion、proportional
傾きー slope、gradient
直線(グラフ)の傾きーslope of the line
図形ーshape、figure
三角形ーtriangle
長方形ーrectangle
台形ーtrapezoid
動かすーmove
兵隊ーsoldier(s)
トランプーplaying cards
女王ーqueen

（数学科　園田毅）