中学1年生1学期、整数論の入り口として、「量」として数をとらえ、ｎ進法や互除法による素因数分解を学んでいきます。ｎ進法、とくに2進法はコンピュータ（電子回路）に利用されていますので、世界で最も使われているｎ進法は10進法でなく2進法であるとも言えます。現在の学習指導要領では、ｎ進法（2進法）は高校の「情報」で学習している内容です。
授業では、22世紀が6進法の世界になっているという設定で、10進法で数えたおはじきを6進法で数えてみることにチャレンジしました。
班ごとに、おはじき約100個、「10」と書いたビニール袋、「100」と書いたビニール袋を配ります。
まず、普通に10進法で個数を数えます。10個ずつ小袋（上写真右）に入れた後、10の小袋を「100」と書いた大袋に入れて数えます。次に、6進法、7進法で数えていきます。おはじき6（7）個を入れた小袋を大袋に6（7）袋ずつ入れて6進法の「100」とすることで、6（7）進法のしくみをつかんでいきます。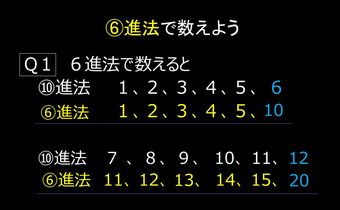
このしくみでいくと、①10進法の36を6進法では「100」と数え、10進法の49を7進法では「100」と数えることになり、10進法より早く位が上がっていくことや、②10進法もそうなのですが6進法で使う数字は「0～5」、7進法では「0～6」となり、ｎ進法で用いる数字は「0～ｎー１」であることも体験として確認できます。
次の授業では、計算で１０進法を6（7）進法で表す方法を考えていきます。その際、この授業でおはじきを6（7）個ずつまとめた経験が計算方法獲得のための原体験になります。6個ずつまとめることは、計算式では「おはじきの個数を６で割る」ことにつながっています。
＜生徒の感想から＞
- 最初は６進法とかはむずかしいと思ったけど、おはじきで分けたらよくわかりました。
- ○進法によっていろいろ教え方がちがっておもしろかったけどややこしくなりました。
- １０でないまとめかたは難しくて、ややこしかった。でも、なれたら楽しくなりそうだ！まとめ方が違うだけで、数字も変わる・・・ふしぎ～
10進法で数えた数を繰り返し6で割るというのが、6進法表示を求めるアルゴリズムなのですが、それはこのような現実の操作を意味しています。学年が上がるにつれて、数学は徐々に抽象的になっていきますが、数式・公式が生まれた背景には現実のできごとがリンクしています。現実と結びつけて理解していくことが、決して早くはありませんが確実に学びが定着するポイントです。私たちは、このことを意識しながら授業づくりを進めていきます。
（数学科 園田毅）
