日本に住んでいる皆さんは毎年夏にセミの鳴き声を聞きますが、アメリカではあたりまえではありません。アメリカには「13年ゼミ」と「17年ゼミ」がいて、彼らはなんど13年に1回、17年に1回だけ、一斉に地上に出てきます。それ以外の年でセミの声を聞くことはないのです。今回の授業では、なぜその数が「13」と「17」という素数なのか考えてみました。
※この授業の構成、紹介資料に関して、以下の文献より引用しています。
「Newtonライト 素数の基本」(ニュートンムック 2018)
吉村仁「素数ゼミの謎」(文藝春秋 2005)
吉村仁「17年と13年だけ大発生?素数ゼミの秘密に迫る!」(サイエンス・アイ新書 2008)
(1)新島襄が見たかもしれない素数ゼミの謎を解いていきましょう。
同志社の創立者新島襄は1865年にアメリカに到着し、岩倉使節団に参加する1872年までアメリカのボストンに滞在していました。ボストンはアメリカ北部にありますので、17年ゼミが生息しています。直近の17年ゼミが現れた2021年、2004年からさかのぼっていくと、なんと1868年が17年ゼミの発生した年にあたりました。新島襄は17年ゼミの大発生を見たり聞いたりしたのではないのでしょうか。
(2)アメリカには「素数ゼミ」以外にも長い周期を持つセミがいました。
実は、昔は12年、13年、14年、15年、16年、17年、18年周期のセミがいたのですが、今は13年と17年周期、素数のサイクルのセミしかいません。
素数ゼミだけがなぜ生き残ったか、この謎を解くカギはそれそれの種類が出会う「周期」にあります。例えば、12年ゼミと14年ゼミが出会う周期、何年に1度地上で出会ってしまうかを計算します。

素因数分解を利用して計算すると、12と14のLCM(最小公倍数)は84です。
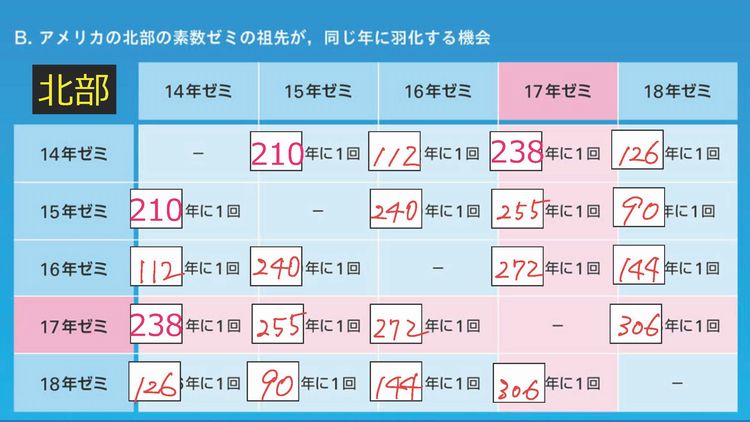
このことは、84年に1度お互い同時に地上に出てくるということを示しています。以前、南部は12-15年周期のセミ、北部は14-18年周期のセミがいました。それらのセミどうしが何年に一度出会うかを、奇数班は北部(17年ゼミがいる地域)、偶数班は南部(13年ゼミがいる地域)を担当してひたすら計算をしました。
(3)素数ゼミと他のセミはなかなか出会えない。
南部と北部に生息していたグループごとに、それぞれのセミどうしがで何年に一度出会えるかを計算して、素数ゼミと出会う機会(次表のピンクの欄)と、それ以外のセミどうしが出会う機会(次表の薄紫の欄)を見比べて、違いを探してみましょう。
少しの例外はありますが、素数ゼミと出会う機会のほうが圧倒的に少ないことがわかります。素数は他の数と共通する約数を1以外持たないので、LCM(最小公倍数)が大きくなってしまうことがおわかりでしょうか。
南部の一覧表です。

計算式です。

(4)素数は、他の数とのLCM(最小公倍数)が大きくなる
何種類かの長い周期のセミの中から、素数年の周期のセミだけが生き残ったのは、「素数は、他の数とのLCM(最小公倍数)が大きくなる」という事実と大きな関係があります。
これにはいくつかの説があります。私からは、日本の生物学者吉村仁さん(静岡大学)の学説を基本に理由を紹介しました。次のスライドにまとめました。

その他にも、外敵とのサイクルの問題、毎年出てくるよりもある年に一斉に大量に発生した方が生き残りに有利、特定の年以外に出てこない理由などについてもさまざまな説、研究が進められています。解説が紹介されているニュース、記事を以下に紹介します。
①数兆匹の大発生も? アメリカで“17年周期ゼミ”羽化始まる
TBS NEWS DIG Powered by JNN
2021年5月報道
②セミは自然界の数学者。13年、17年周期で大発生! その驚きのワケとは・・・
~セミが身につけた生き残るための秘策~
https://gendai.media/articles/-/37696
2013年12月6日
③セミと素数の関係【素数ゼミ】
youtube 予備校のノリで学ぶ「大学の数学・物理」
https://youtu.be/6axMxUS-qgQ
下のスライドの参考文献もご紹介します。
今回は、素数と自然界の身近な関係が身近にある例を知りました。
(数学科 園田毅)




