
日本に住んでいる皆さんは毎年夏にセミの鳴き声を聞きますが、アメリカではあたりまえではありません。アメリカには「13年ゼミ」と「17年ゼミ」がいて、彼らはなんど13年に1回、17年に1回だけ、一斉に地上に出てきます。それ以外の年でセミの声を聞くことはないのです。今回の授業では、なぜその数が「13」と「17」という素数なのか考えてみました。
※この授業の構成、紹介資料に関して、以下の文献より引用しています。
「Newtonライト 素数の基本」(ニュートンムック 2018)
吉村仁「素数ゼミの謎」(文藝春秋 2005)
吉村仁「17年と13年だけ大発生?素数ゼミの秘密に迫る!」(サイエンス・アイ新書 2008)

(1)アメリカには「素数ゼミ」と呼ばれるセミがいます。
2021年6月に報道されたニュースをご紹介します。
「なぜ? 17年に1度…セミが大量発生! “限定チョコ”も登場 アメリカ」(2021年6月2日放送「news every.」より)
https://youtu.be/StTlO_BK1L0
このニュースでも紹介されましたが、アメリカには13年周期と17年周期のセミがいて、日本と違って毎年地上に出てきません。南部では13年に1度、ワシントンやニューヨークのある北部では17年に1度、地上に出てきて鳴きます。北米では2004年、2021年に発生し、次は2038年に出てきます。アメリカでは、夏にセミが現れることがニュースになるのです。
実は、昔は12年、13年、14年、15年、16年、17年、18年周期のセミがいたのですが、今は13年と17年周期、素数のサイクルのセミしかいません。
今回の授業は「なぜ、素数の周期のセミが生き残ったのか」について考えてみました。
ちなみに、このセミは鳥も人間も食べています。レストランに「セミフライ」がメニューとして売られているそうです。私は食べられそうな気がしますが、皆さんはどうでしょうか。
(2)2つの周期のLCM(最小公倍数)の計算
素数ゼミがなぜ生き残ったか、この謎を解くカギはそれそれの種類が出会う「周期」にあります。例えば、12年ゼミと14年ゼミが出会う周期、何年に1度地上で出会ってしまうかを計算します。

素因数分解を利用して、12と14のLCM(最小公倍数)を考えます。
LCMは84です。これは、84年に1度お互い同時に地上に出てくるということを示しています。
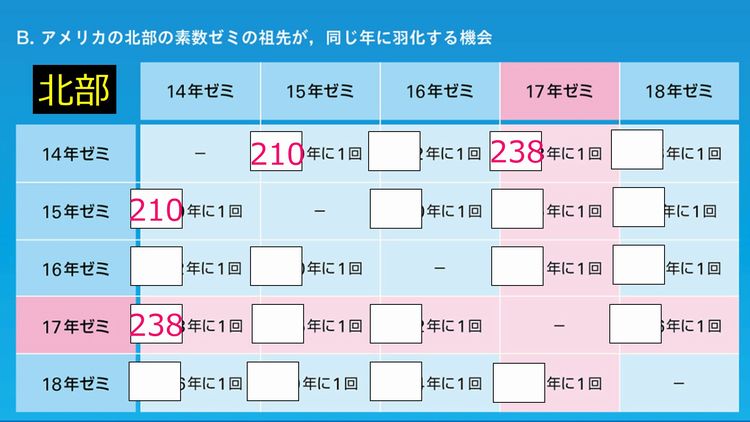
以前、南部は12-15年周期のセミ、北部は14-18年周期のセミがいました。それらのセミどうしが何年に一度出会うかを、奇数班は北部(17年ゼミがいる地域)、偶数班は南部(13年ゼミがいる地域)を担当してひたすら計算をしました。

(3)新島襄は素数ゼミを見たのだろうか?
余談になりますが、同志社の創立者新島襄は1865年にアメリカに到着し、岩倉使節団に参加する1872年までアメリカのボストンに滞在していました。ボストンはアメリカ北部にありますので、17年ゼミが生息しています。直近の17年ゼミが現れた2021年、2004年からさかのぼっていくと、なんと1868年が17年ゼミの発生した年にあたりました。新島襄は17年ゼミの大発生を見たり聞いたりしたのではないのでしょうか。このことを授業で紹介すると、生徒さんからは「それだったら、新島襄は日記に書いているはずだから見てないと思う。」と指摘されました。同中生ならではの発言ですが、新島襄が見ていたかもしれないと思うと、あらためて素数ゼミに親しみがわく話題でした。



