2021年11月、1次関数を表記する3要素「式」、「対応表」、「グラフ」を結ぶ教材として、「1次関数トランプ」を作成し、授業でゲームを実施しながら学習しました。
例年、本校では「正負の数」、「平方根」の学習で、カードゲームを活用した授業を実施しています。が、コロナ禍の2年間はグループ活動を制限(とくにモノの共有)したため、しばらくこのような「数学的活動」ができないでいました。11月より制限を緩和して、短時間(15分間程度)、机を合わせてなるべくしゃべらないようにして、「1次関数トランプ」を行いました。
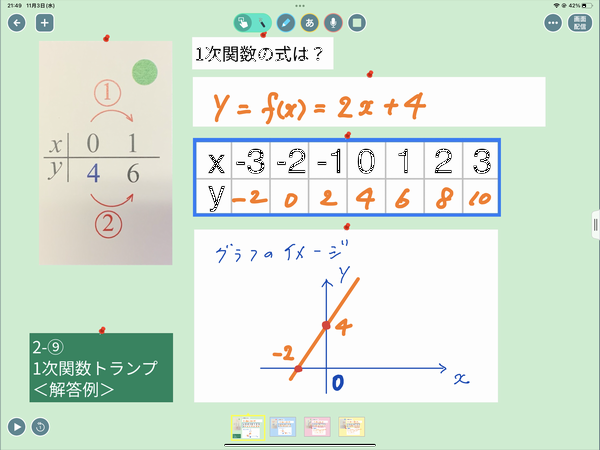
授業の前半では、ロイロノート配信で1枚のカード(対応表)から、関数の「式」とグラフの概形を書いて前時までの復習を行いました。(中学生にとっては、xy座標上に描かれたグラフから関数の「式」を「復元」するのが難しいです。)今回は、1次関数の4つの表記をトランプのスートのようにして、①関数の式、②対応表、③グラフ、④比例定数(傾き)・初期値(y切片)に慣れるのが目的です。写真では「y=f(x)=2x+4」の例を表していますが、それぞれの表示の中の「比例定数(傾き) 2」と「初期値(y切片) +4」がつながって、比例定数が正だからグラフが右上がりだとか、y切片が正だから原点より上でy軸と交わっていることが、カードゲームを通しての実体験として理解してもらえればうれしいです。
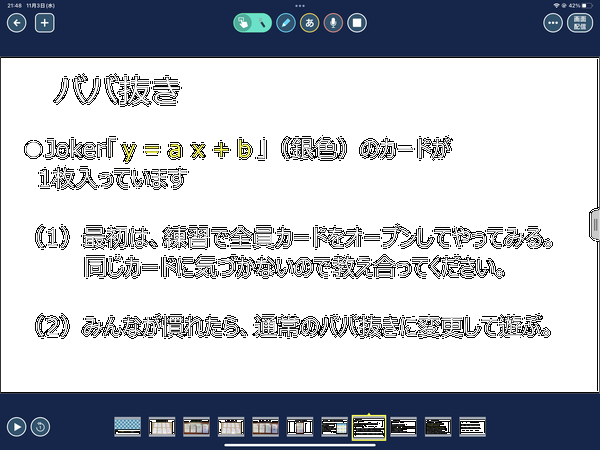
授業の後半では、トランプのカードのしくみやゲームの進行方法をプレゼンして(PowerPointからロイロノートへエクスポートして作成)、4人1グループでゲームを始めました。最初は、ババ抜きの手札を公開したがら(隣の人と見せ合いながら)、どれとどれが同じ関数を表しているかを理解しながら進行するようにしました。慣れたら、普通のババ抜きへ移行しました。
「1周回るのが早いので、揃っているか確認するのが難しかったけど、楽しかったです。」
「考える時間が必要だったので疲れた。」
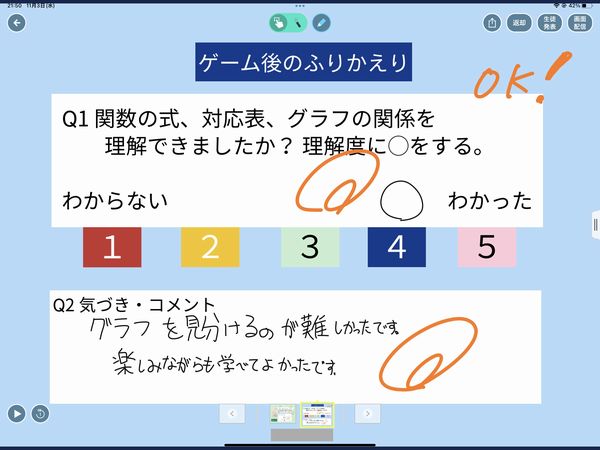
「グラフを見分けるのが難しかったです。」
「関数の式で表すとき、xが0の時にyが0でなければ何かをその関数に足すか、引かなければ
ならないということがわかった。」
「じっくり見ないとわからない。」
「同じカードを探すのに時間がかかるけど、楽しかった。少し難しい。」
「初めは大混乱だったけれど、慣れてくるととても楽しかったです。遊びながら勉強できるので一石二鳥だなと思いました。」
など、うれしいコメントが寄せられました。
※今回作成、使用した「1次関数トランプ」カードのアイデアとデータは嘉摩尻寿氏(和歌山県 中学校数学教員)によるものです。
(数学科 園田毅)