本校中学1年生の田中一奨さんがscratch(スクラッチ)で作った互除法のプログラムを、以下にご紹介します。
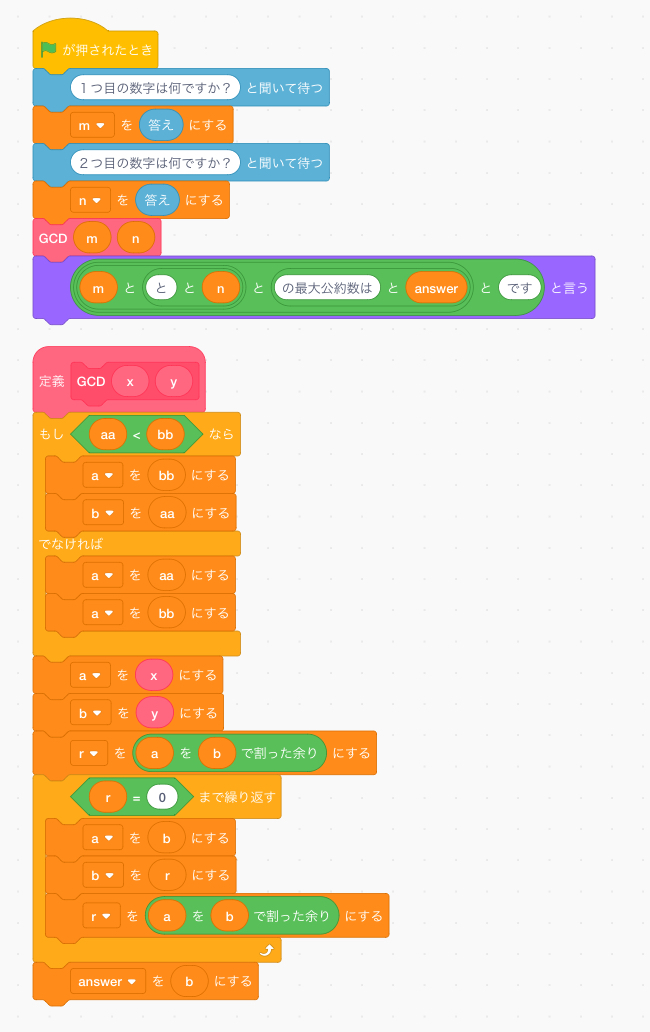
私は、同じ互除法のプログラムをExcel VBA(Vixual Basic for Aplications)で作ってみました。
以下のコードです。

このテーマの記事で何度も紹介しておりますが、「互除法」で2数のGCD(最大公約数)を求める計算方法を以下に再掲します。

私は自分が使い慣れているExcelを使って作りました。一方、中学1年生の何人もの方が私の授業での呼びかけに応じてくださり、小学校やプログラミング教室で学ばれたscratch(スクラッチ)で主に作られていました。
これまで、中学数学で学習するGCD(最大公約数)の求め方と言えば、素因数分解を使うのが「常識」でした。覚えている大人の方も多いと思います。しかし、素因数分解できる自然数は人が思いつく範囲で解くとき(出題するとき)、2、3、5、7といった1桁の素数(もう少し加えてもせいぜい11、13、17まで)で割れる自然数に事実上限られます。素因数分解の難しさは、コンピュータも同じです。余談になりますが、コンピュータも人間同様、素数を順にあてはめて、割り切れるかどうかを試しています。数十ケタ程度の整数ならあっという間に素因数分解することができますが、数百ケタの素数どうしのかけ算でできている整数を素因数分解することはコンピュータでも膨大な時間がかかるのです。ちなみに、インターネットの通信販売でやりとりされるクレジットカードの番号などの個人情報を守る「RSA暗号」は、このこと(コンピュータでも時間がかかること)を利用して作られたものです。
GCD(最大公約数)のお話に戻りましょう。
素因数分解を使う方法と比べ、互除法は2数を割る計算の繰り返しですので、共通の約数に大きな素数が入っていても必ずGCD(最大公約数)が求められます。私自身、今までは素因数分解が「王道」で、互除法はややマニアックな解き方のイメージを持っていましたが、コンピュータが普及し、小学校でプログラミングの基礎を学ぶ現在、両者の立ち位置は逆転するように感じています。
(数学科 園田毅)



