互除法によって2数のGCD(最大公約数 Greatest Common Devisor)を求める考え方をわかりやすくご紹介します。

計算の流れを再掲します。
180と252のGCD(最大公約数)を互除法によって求める計算は次のような手順です。
①252を180で割って、1余り72が出ます。
②180を①の余り72で割って、2余り36が出ます。
③72を②の余り36で割ると、2でちょうど割り切れます。
④計算が割り切れたときの「割る数 36」が、180と252のGCDとなります。
これが互除法です。どのような2数でも割り切れるまで計算すれば、必ずGCDを求めることができます。
授業では、180と252をタテ・ヨコとする長方形を最も大きな正方形で埋め尽くす(敷き詰める)ことができれば、その正方形の1辺の長さが2数のGCD(最大公約数)になるはずというイメージで説明しました。(2数を2本のテープの長さと考える説明方法もあります。)

上記は、中学生の皆さんが解いた計算の板書です。(2022年10月)
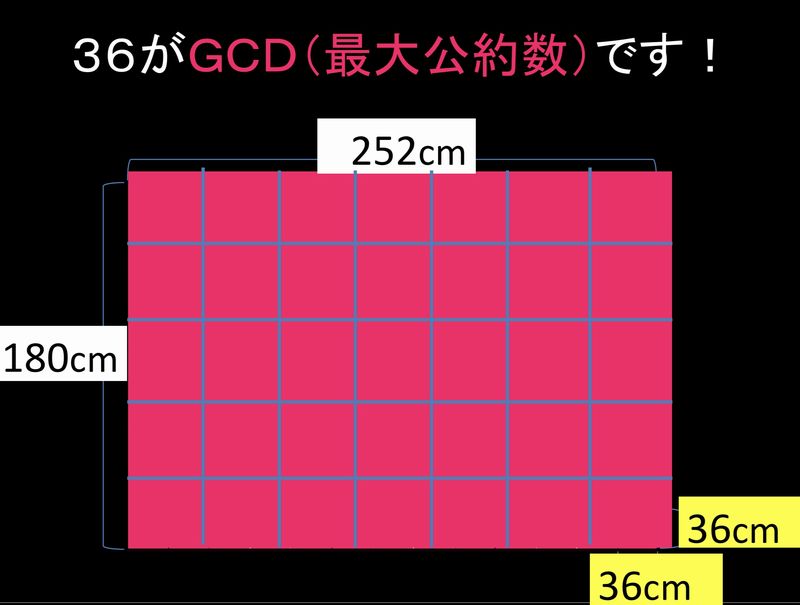
この1辺36の正方形を見つけることが互除法の操作的な意味です。以下、お手元に180mm×252mmの長方形の紙(ほぼB5サイズ)があると考えながらお読みください。
互除法は大きい方の数が小さい方の数で割り切れるまで、計算を繰り返していきます。今回は例題を2つ示します。180と252操作と実際の計算)は次回の記事でご紹介します。
<例1>
72と18の長方形で、大きい方の数72を小さい方の数18で割ると、商が4、余りが0になります。これは、この長方形は1辺18の正方形4枚分となり、GCDが18であることを示しています。
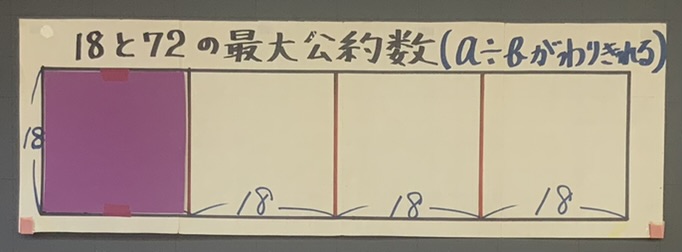
式で表すと、
72÷18=4 (余り0)
となり、72と18のGCDは18です。
<例2>
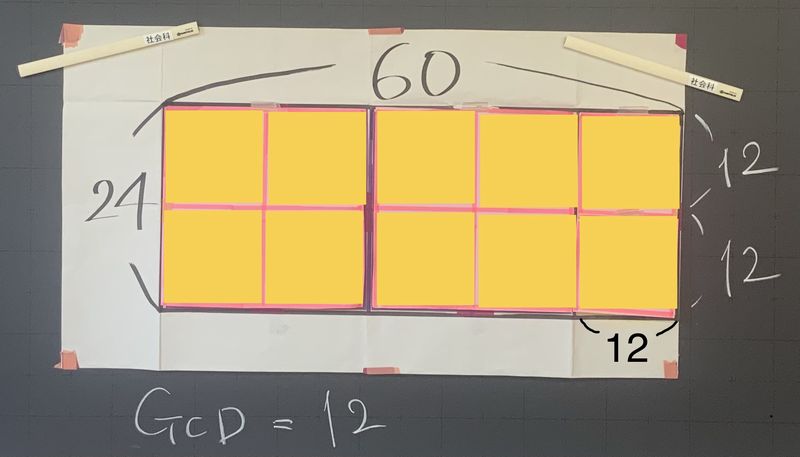
60×24の長方形で、大きい方の数60を小さい方の数24で割ると、商が2、余りが12となります。これは、この長方形から1辺24の正方形が2枚取れて、24×12の長方形(写真内黄色の図形)が余ることを意味しています。
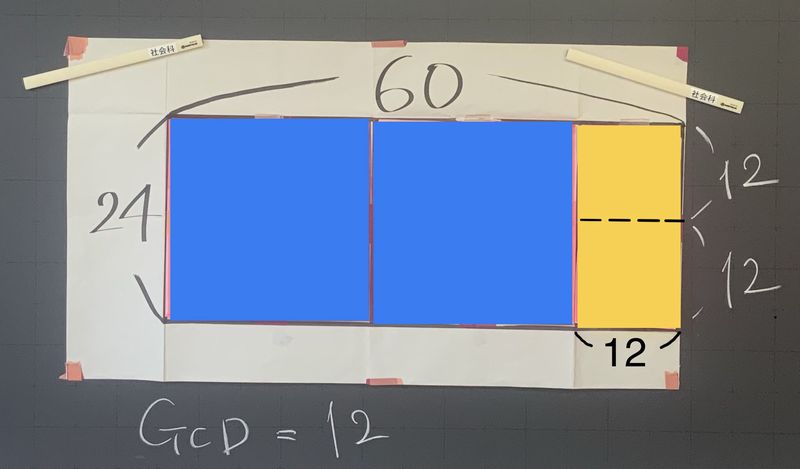
次に、正方形が切り取れなかった24×12の長方形では、1辺12の正方形がぴったり2つ取れます。結局、元の60×24の長方形から、1辺12の正方形がタテ2列、ヨコ5列、合計10枚、ぴったり取れることがわかりました。
この2回の操作を式で表すと、
60÷24=2 余り12
24÷12=2 (余り0)
となり、60と24のGCDは12です。
この2例で、互除法の基本的なアルゴリズムを説明してみました。
(数学科 園田毅)



