連載(1)の2つの例題で、互除法の基本的な解き方のしくみ(アルゴリズム)をざっくり説明してみました。
今回は、授業で取り上げた、180と252の最大公約数(GCD)を互除法によって求めるアルゴリズムを、タテ180、ヨコ252の長方形を示しながらご紹介します。
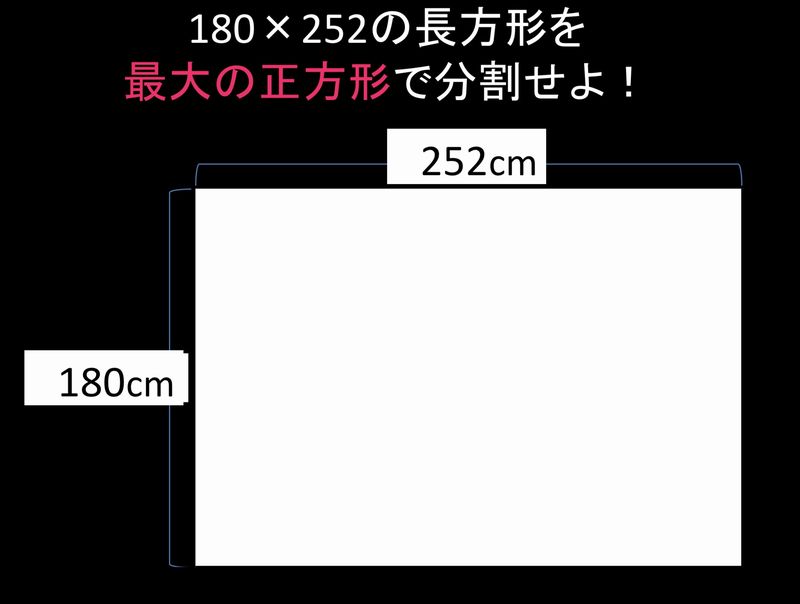
まず、252を180で割って、180の正方形でちょうど敷き詰められるかを確認します。もちろん、切り取れないです。①252を180で割って、1余り72が出ます。
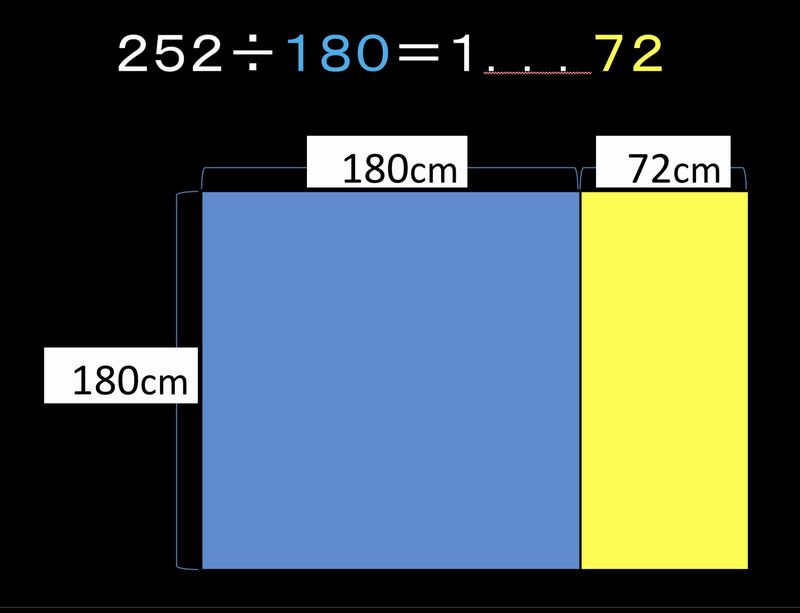
この計算は、1辺180の正方形が1つ取れて、右側に180×72の黄色の長方形が余っていることを示しています。
次に、黄色の長方形が1辺72の正方形で敷き詰められるか考えます。
②180を①の余り72で割って、2余り36が出ます。
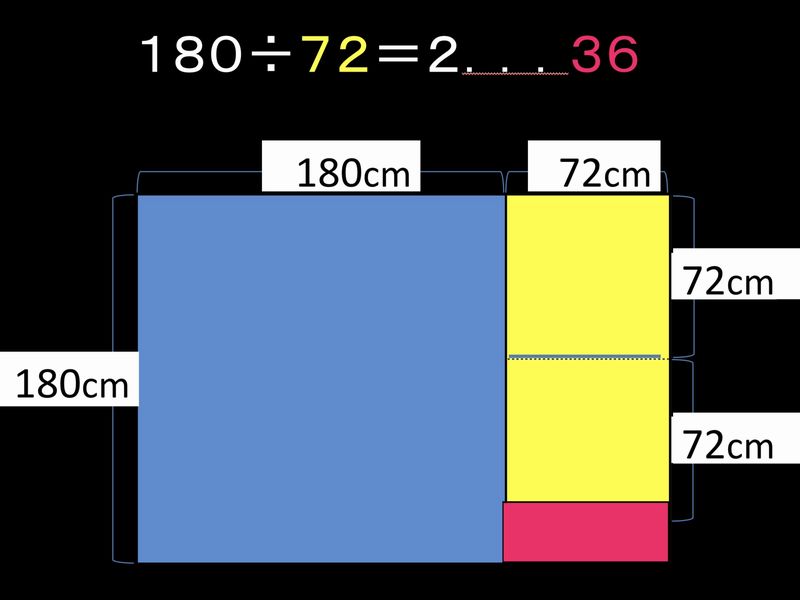
この計算は、1辺72の正方形が2つ取れて、右下側に36×72のピンクの長方形が余っていることを示しています。
次に、ピンクの長方形が1辺36の正方形で敷き詰められるか考えます。
③72を②の余る36で割ると、2でちょうど割り切れます。
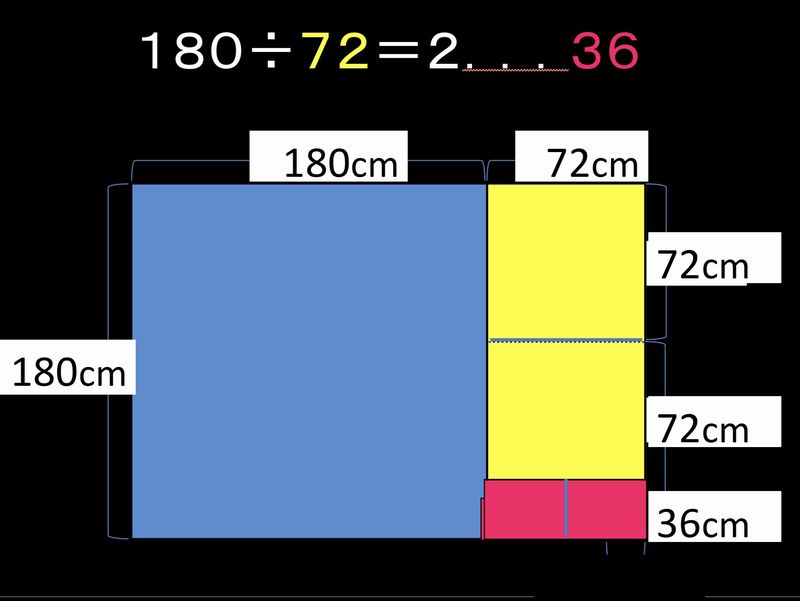
この計算は、ピンクの長方形が、1辺36の正方形2つで敷き詰められたことを示していて、さらに、元々の180×252の長方形が、1辺36の正方形で敷き詰められることを意味しているのです。
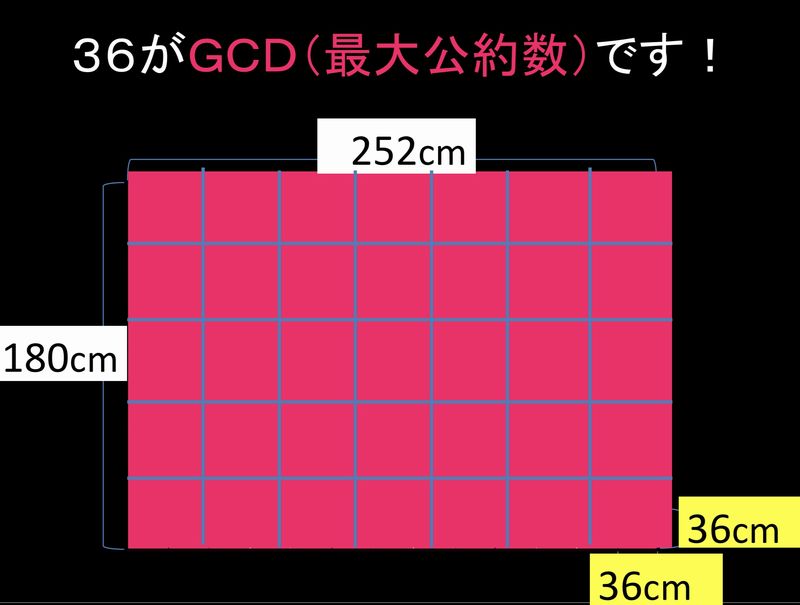
計算が割り切れたときの「割る数 36」が、180と252の最大公約数(GCD)となります。
これが互除法です。どのような2数でも割り切れるまで計算すれば、必ず最大公約数(GCD)を求めることができます。
授業では、実際に180mm×252mmの紙を渡して、順に正方形を作りながら(対角線を折って正方形を折り、書き込みながら)、36mmの正方形が2つできるところまでを体験しました。
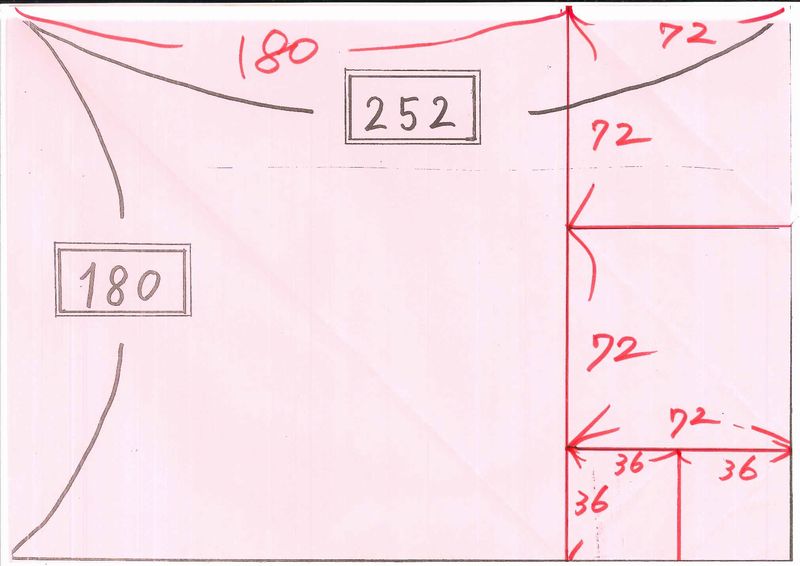
(数学科 園田毅)



