中1数学2学期、図形の学習では、手作り分度器「カクシリキ」で学内外の階段他、いろいろなモノを測りました。次の授業では、グループに分かれてテーマ別レポートを作成してもらいました。
今回、ご紹介する授業は「角度」についての学びの最終回、学校から比叡山を見上げた角度(仰角)を測って、学校から約4km離れている比叡山(写真)の高さを求めたものです。
カクシリキを使っての計測で、木のてっぺんが45度になるように移動して学内のイチョウの高さを測る体験をしてきました。直角二等辺三角形の性質を利用して、木に登らずとも高さを測る工夫です。しかし、直角三角形は45度でなくても、直角をはさむタテとヨコの辺の長さの比は決まっています。高校数学で学習する「三角比」(タンジェント tanθ)です。つまり、目標物への仰角と水平距離がわかれば、タンジェントを用いることによって、仰角を45度にして見られない遠くの山の高さを求めることができます。今回は、学校から約4km離れている比叡山の高さを、三角比表を使って求めてみました。
 左図は中学校から見える比叡山、下図は、そのイメージ図
左図は中学校から見える比叡山、下図は、そのイメージ図
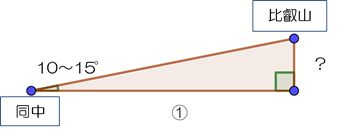
先回の記事で紹介した、角度を表す「%」(車道の傾斜)、「‰(パーミル)」(線路の傾斜)、「三寸勾配(さんすんこうばい)」(屋根の傾斜)はすべて直角三角形の「タテ÷ヨコ」、すなわちタンジェント(tanθ)です。ヨコの長さ①あたりのタテの長さです。三角比・三角関数は現在高校で学ぶことになっていますが、よく考えると中学生の日常生活の中にもその元となる事象は多くあるわけです。中学数学で学ぶ比例・1次関数のグラフの「傾き」はまさにタンジェントの別の表現です。中学生まではタテとヨコが1:1となる45°という特別な角度だけを扱ってきましたが、タンジェントを「ヨコを①としたときのタテの長さ」と伝えれば中学生も十分理解できます。
さらに、学校の階段について調べたグループのレポートで、建築基準法では角度の上限(小学校32度、中学校35度)とともに、一段の奥行き(踏み面)と高さ(蹴上げ)が定められていることを知りました。まさにタンジェントです。そして、2021年度から始まった「大学入学共通テスト」では2回連続で三角比表が使われました。いわゆる受験数学では、三角比・三角関数の学習の中で30°45°、60°といった特別な角度が強調される印象があります。が、本来三角比・三角関数は特別な角度に限らず、どの角度でも辺々の比が決まっていることが大事で、それを前提に使われ、学問が発展してきました。三角比表があることの便利さを実感してほしいところです。
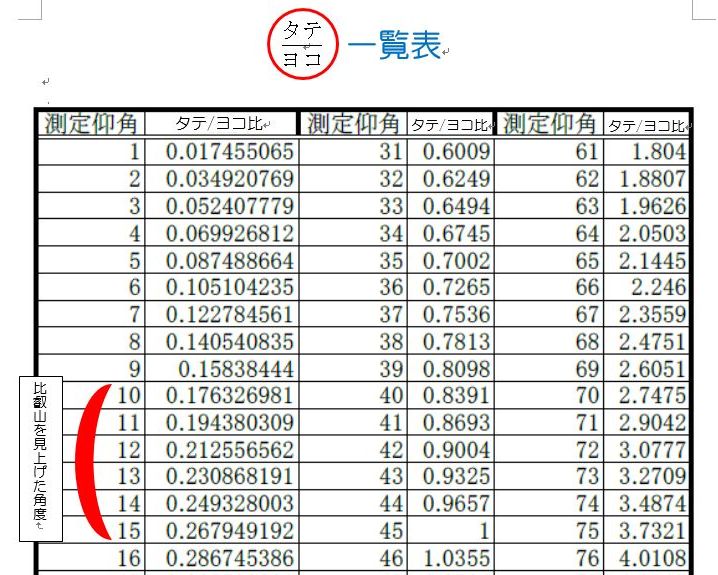
中学生の皆さんが自作のカクシリキで測った、学校から見上げた比叡山の角度(仰角)はだいたい10~15°になります。あとは水平距離ですが、これはYahoo地図、GoogleEarthを使って、約4000~4300m程度と調べてもらいました。授業プリントには本当の高さに近い11°(タンジェントは0.194…なので、0.19ないし0.2で計算しています)を記載しましたが、各自が測った仰角と水平距離で求めていきました。数は生徒さんのプリントの一部です。
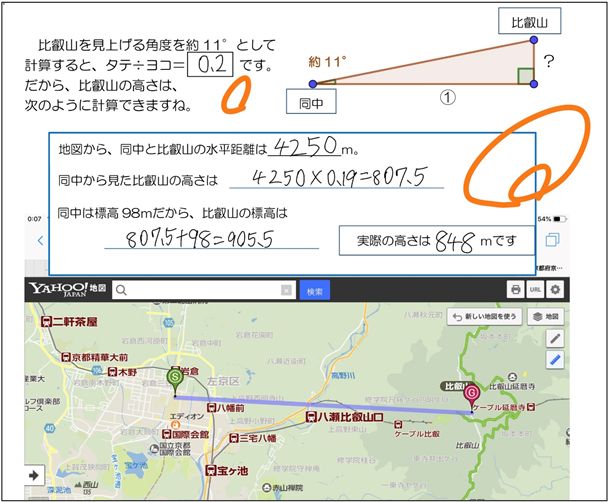
中学生の皆さんには、今回用いた「タテ÷ヨコ」の値が、①グラフの「傾き」、②スロープや道路・線との傾斜を表す「分数」、「%、‰(パーミル)」表記、③三角比(tanθ)と同じものであることを、今後ざっくり理解していってほしいと思っています。
(数学科 園田毅)



