同志社創立記念日の11月29日を4ケタの数で表すと、1129は素数です。西暦を含めた20191129は、7×19×151813と素因数分解できるので素数ではありません。

今まず、前回のブログで説明したことを簡潔に紹介します。(3)からが今回の内容です。
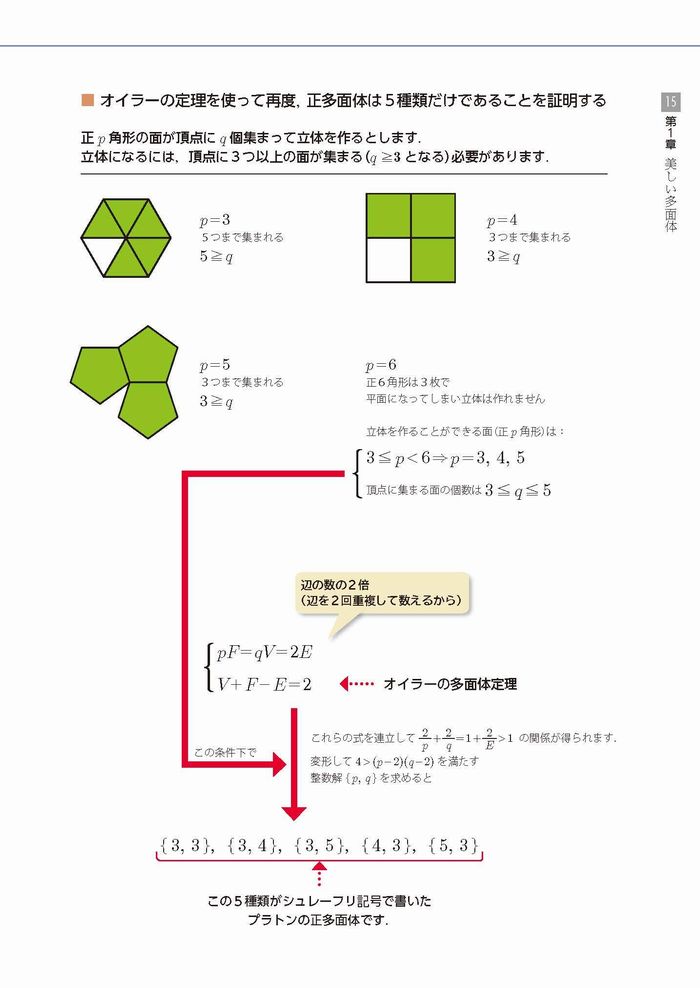
(1)ある条件をクリアした立体(多面体)は、「オイラーの多面体公式」が成り立っています。
(面の数)+(頂点の数)-(辺の数)= 2 ・・・①
(2)正多面体の面の形をp角形(pは3以上の整数)、頂点に集まる面の数をq(qは3以上の整数)とすると、次の関係が成り立っています。
(ⅰ)(面の数)=(辺の数)×2/p ・・・②
(ⅱ)(頂点の数)=(辺の数)×2/q ・・・③
(3)②、③の結果をオイラーの多面体公式①に代入します。
(辺の数)×2/p+(辺の数)×2/q-(辺の数)= 2
両辺を(辺の数)で割って、
2/p+2/qー1 = 2/(辺の数)
(4)次に、急に不等号が入ります。
2/p+2/q-1 = 2/(辺の数) > 0
2/p+2/q-1 > 0
両辺にpqをかけて、式を整理していきます。
2q+2p-pq > 0
両辺に-1をかけて、
pq-2p-2q < 0
最後に、左辺を因数分解するためのテクニックで両辺に4を加えます。
pq-2p-2q+4 < 4
(p-2)(q-2)< 4
(5)pはp角形のp、qは頂点に集まる面の数のことでした。そして、p、qともに3以上の整数です。この条件でpとqのペアを考えると、
(p、q)=(3、3)、(3、4)、(3、5)、(4、3)、(5、3)
の5通りしかありません。左のペアから順に、正4面体、正8面体、正20面体、正6面体(立方体)、正12面体を意味しています。
(数学科 園田毅)

“Only 5 kinds of Regular polyhedron! 4”
I will introduce briefly what I explained in the last blog. I will explain the contents from section (3) this time.
(1) “Euler’s polyhedron formula” is established for solids that have some contents.
(the number of faces)+(the number of vertices)-(the number of sides)=2・・・ ①
(2) When the shape of regular polygons is “p” (p ≥ 3) and the number of faces is “q” (q ≥ 3),
(ⅰ) (the number of faces) = (the number of sides) × 2/p ・・・ ②
(ⅱ) (the number of vertices) = (the number of sides) × 2/p ・・・ ③
(3) Insert the result of ②, ③ into Euler’s polyhedron formula
(the number of sides)×2/p+(the number of sides)×2/qー(the number of sides) = 2
Divide both sides of the equality by the number of sides.
(Faces)+(Vertices)ー(Sides) = 2
2/p+2/qー1 = 2/(the number of sides)/p>
(4) Here, add an inequality sign to the expression.
2/p+2/qー1 = 2/( number of sides) > 0
2/p+2/qー1 > 0
Multiple both sides of the equality by pq and simplify the expression.
2q+2pーpq > 0
Multiple both sides of the equality by -1
pqー2pー2q < 0
Finally, add both sides of the equality by 4 as a technique to factorization.
pqー2pー2q+4 < 4
(pー2)(qー2) < 4
(5) p is a p-sided polygon, q is the number of faces gathering at a point. In addition p and q are integer more than or equal to 2. Considering this condition, we have “only 5 kinds” of solutions.
(p, q) = (3, 3), (3, 4), (3, 5), (4, 3), (5, 3)
The answer means tetrahedron, octahedron, icosahedron, cube and dodecahedron from left to right.
Mathematics is wonderful and mysterious because we can know the truth by only calculations even though we don’t have real things in front of us.
by Tsuyoshi Sonoda (Math Dept.)
谷克彦「美しい幾何学」(技術評論社 2019)より