本日2月27日を3ケタの数で表した227は素数です。西暦を含めた20190227も素数になります。
前回、正多面体はたった５種類、正四面体、正六面体（立方体）、正八面体、正十二面体、正二十面体しかないことを紹介しました。今日は、その解答編です。
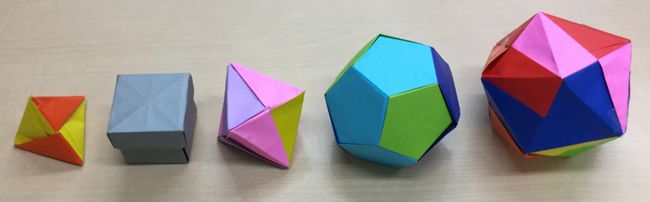
ポイントは2つです。1つ目は、正多角形が3枚以上でないと立体の角（かど）を作ることはできません。もう1つは、角に集まる正多角形の角度の合計は360度未満でなければなりません。
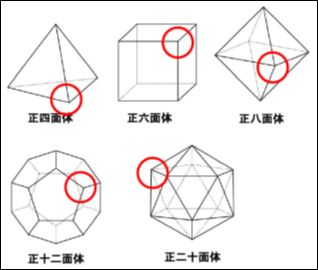まず、正六角形で正多面体を作ることは不可能です。正六角形の１つの内角は120度なので、１つの頂点に正六角形が３枚集まるとその角度の和は360度となり、角が平らになって正多面体を作ることはできません。そうです。角に集まる正多角形の角度の和が360度より小さくならないと、尖った角ができないのです。
次に、正三角形、正方形、正五角形の場合を考えてみましょう。
１つの頂点に正三角形が３枚ずつ集まると正四面体、４枚ずつ集まると正八面体、５枚ずつ集まると正二十面体ができます。が、正三角形６枚の角度の和は360度なので、これ以上の枚数の正三角形で正多面体を作ることはできません。
１つの頂点に正方形が３枚ずつ集まると正六面体ができますが、正方形の１つの内角は90度なので、正方形４枚の角度の和は360度なので、これ以上の枚数の正方形で正多面体を作ることはできません。
１つの頂点に正五角形が３枚ずつ集まると正十二面体ができますが、正五角形の１つの内角は１０８度なので、正五角形４枚の角度の和は360度以上となり、これ以上の枚数の正五角形で正多面体を作ることはできません。
これが、正多面体が５種類しかない理由です。
（数学科 園田）
“Only 5 kinds of Regular polyhedron! 2”
I talked about how there are only 5 kinds of regular polyhedron, tetrahedron, cube, octahedron, dodecahedron and icosahedron in the last blog. I will show the reason this time.
There are 2 points. One is that we can make verities by more than 3 polygons. The other is that the sum of angles of regular polygons gathering at a point are less than 360 degrees.
First, it is impossible to make a regular polyhedron by regular hexagons. An interior angle of a regular hexagon is 120 degrees. The sum of the angles of 3 regular hexagons gathering at a point are 360 degrees. So 3 regular hexagons can’t make a vertex because those get to be flat.
You know that we can make a corner where the sum of angles are less than 360 degrees.
Next, we think about triangles, squares, pentagons. We can make tetrahedron by 3 regular triangles, octahedron by 4 regular triangles, icosahedron by 5 regular triangles gathering at a point. But the sum of the angles of 6 regular triangles are 360 degrees, so we can’t make polyhedron with more than 6 regular triangles.
We can make cube by 3 squares gathering at a point, but the sum of the angles of 4 squares are 360 degrees , so we can’t make polyhedron with more than 4 squares.
We can make a dodecahedron by 3 regular pentagons gathering at a point, but the sum of the angles of 4 regular pentagons are over 360 degrees, so we can’t make polyhedron with more than 4 regular pentagons.
This is why there are only 5 kinds of regular polyhedron.
by Tsuyoshi Sonoda (Math Dept.)
