2024年1月より、数学アプリ「GeoGebra6(Classic 6バージョン)」の「検定」を始めました。毎回30-40 分間の講座を5回シリーズで6級から1級へ、そしてMaster取得まで予定しています。(1級とMasterは新年度に実施予定です。)
GeoGebraの優れているところは手書きでは時間がかかるような複雑な図形やグラフを簡単にかつ正確に描くことができ(立体も!)、さらにいろんな条件に応じて動かすことができることです。お家のPCでもやってみようという方は「全機能統合版・Classic 6」がおすすめです。

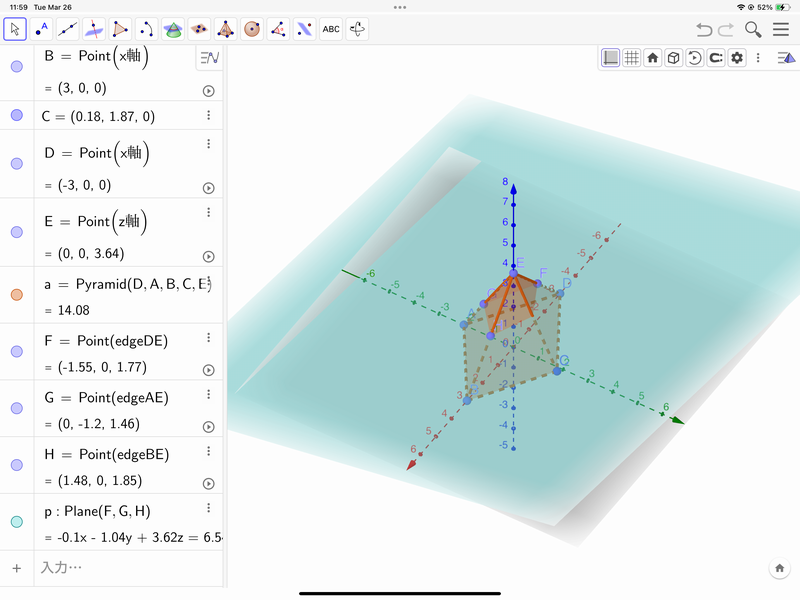
3/26tue.午前、6回目2級講座「空間図形」、準1級講座「空間図形」を使う、を連続で実施しました。春休みに4名の皆さんが参加されました。講師は数学科の児玉さんです。
2級講座では、正多面体と球を、コードを使って描きました。正多角形を1つ作ってから、正多面体の英語名を入力して簡単に作ることができます。例えば、正4面体は、「tetrahedron(点,点,点)」、または、「tetrahedron(三角形)」、と入力すると3次元座標に立体が現れます。「三角形」は例えば「poly1」などの名前です。また、入力画面には「tetrahedron(poly1,true)」というふうに、デフォルトでは「true」と表示されます。これを「false」にすると、先ほどできた立体と鏡像になる立体ができます。参考に、他の正多面体もコードを紹介します。
正6面体(立方体) cube
正8面体 octahedron(三角形)
正12面体 dodecahedron(五角形)
正20面体 icosahedron(三角形)
続いて、球を描きました。「中心と通る点で決まる球面」、または「中心と半径で決まる球面」というアイコンを使って描けます。私も含めて皆さんが半径をなんとなく3~5あたりにするところ、お1人だけ「23」にした方がおられて、3次元座標の画面を見る視点が球の内側にある状態となり、おもしろかったです。画面をピンチアウトすると、球を外側から見る視点に変わりました。

続いて、準1級です。準1級は「空間図形」の発展操作で、角錐・角柱、円錐・円柱、円弧、扇形などを描きました。
角錐・角柱、円錐・円柱は、複数の描画方法で描いてみて、さらに、点をドラッグすることで、一度描いた立体の形や高さを変えたりすることを学びました。最後に、立体の切り口を見たいという要望があり、立体を分割する平面を描いてその切り口を確認することができました。
次回(4月)は、1級「動点(1次関数)と範囲指定のグラフ」、Master「動点(2次関数など)とテキストボックスの応用」です。中学受験で、長方形の中を点が動くような問題にとりくんだ方もおられると思います。それです。
お楽しみに!
(数学科 園田毅)