折り紙で5種類の正多面体を折りました！

MATH@DJHS / 2022.7.25

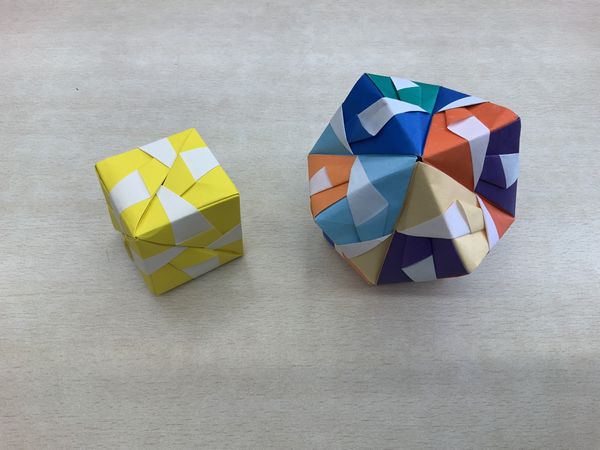
7月11日（月）からのフォローアップ期間から終業式まで、折り紙シリーズの学プロ4回で、折り紙で5種類の正多面体を折りました。

正多面体は全部で5種類しかありません。そのことは、紀元前4-5世紀、古代ギリシャの哲学者プラトンの時代からすでに知られていました。正4面体、正8面体、立方体（正6面体）、正12面体、正20面体の5種類です。今回、ご紹介した折り方は、同じユニットを折れば正4面体、正8面体、正20面体が折れるものでしたので、折り方は3種類マスターすれば全て折れます。正4面体は2枚の折り紙で作れます。立方体は6枚、正8面体は4枚、正12面体は12面体、正20面体は10枚の折り紙が必要です。正20面体以外は組み合わせ方がスムースに進めば、30－40分程度で完成できると思います。正20面体は10枚折るのもたいへんですが、初めての方は組み合わせ方が少し難しいと思います。

正多面体がなぜ5種類しかないのかという問いは、小学校6年生から中学1年生にとって、おもしろい「数学的活動」、問題発見の課題です。折り紙でなくても（ポリドロン等各面を組み立てる教材もあります）、自分で実際に作ってみることから学びが始まるテーマです。それぞれの多面体の面の形や頂点付近の様子を注意深く観察することが求められます。数学に限りませんが、問題解決には「分析と総合」が必要です。正多面体が5種類であるという問題の解決には、立体を面・線・点それぞれのパーツを観察（分析）し、その気づきをつなぐ（総合する）ことがまさに「分析と総合」にあたります。