2022年5月6日(金)、学びプロジェクトで正十二面体カレンダー(06/2022-04/2023)を作りました。正五角形2つの図から設計図が簡単に作れてしまうのが、この工作のおもしろいところです。参加者の皆さんには、学校で資料(A3とA4の型紙、説明プリント)をお渡しして、ご自宅からオンライン参加してもらいました。最初に、私から設計図の作り方を紹介し、その後、ハサミ、のり、マスキングテープを使って自作してもらいました。
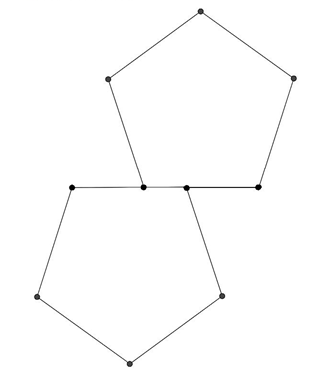
A3の型紙には正十二面体の展開図にカレンダーが印刷されていて、切り取って組み立てれば完成できます。そして、展開図の作り方を、A4の型紙に書かれている2つの正五角形で説明しました。ちなみに、この展開図は、中学生の皆さんのiPadにも入っている「GeoGebra」というアプリで作っています。
なお、このアイデアは、京都先端科学大学附属中学校高等学校教諭 山脇孝之さんにご教示いただいたものです。
(1)正五角形の5本の対角線を引くと、正五角形の中心に、対角線でできた小さな正五角形ができてくるのがおわかりになると思います。(右下図)
(2)今度は、正五角形の中心にできた正五角形の対角線を引いてみます。すると、左下図のように最初の正五角形の内部に、小さな正五角形が6つできたことが確認できます。この用紙には正五角形が2つ書いてあったので、小さな正五角形が合計12個できたわけです。これで、正十二面体の展開図ができあがりました。
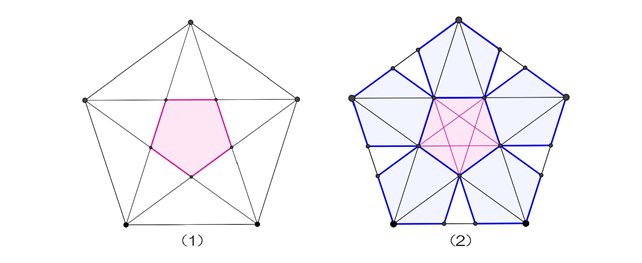
今回は詳しくお話していませんが、対角線を書き込んだ図をよく見ると、中心の小さな正五角形の中心にさらに小さな正五角形が見つけられると思います。内部の正五角形の対角線を書いていくと、その内側にどんどん正五角形ができていくのです。また、元の辺の長さと、内側の正五角形の辺の長さにも「黄金比」と呼ばれるおもしろい関係があります。また、皆さんといっしょに学んでいきたいと思います。ご参加、ありがとうございました。
(数学科 園田毅)