2024年2月21日、京都町屋科学館の倉橋さんが、錯視の1種類である「アナモルフォーシス」について学びプロジェクトを企画してくださいました。立志舘2階、ピタゴラス教室(数学1)で実施しました。お2人の中学生が参加、体験されました。
京都町屋科学館:https://tsukuru-manabu.jp/


多くの皆さんが博物館、科学館へ行ったときに、ゆがんだ図を円筒形の鏡に映すと正常な形に見える展示を体験したことはないでしょうか。それが「アナモルフォーシス」です。
アナモルフォーシスは錯視の1つで、円筒形や円すい形の鏡(アクリル製の鏡は100均などで手軽に買って作れます)に映すと正常な絵が見えるものです。直交座標(中学数学の授業で出てくるxy座標のこと)と極座標の変換が原理になっています。アナモルフォーシスの原理は数学の学習と密接な関係があって、一番身近な単元は相似(中学)や座標変換(高校)です。
今回は、京都町屋科学館から持ってきてくださったアインシュタインやミッフィーを題材にしたアナモルフォーシス、2枚の鏡の角度でモノが複数に分裂して見える装置(万華鏡の原理ですね)、2次関数のグラフの焦点の性質を利用した凸面鏡の上に物が浮かんで見える展示物を見せていただきました。

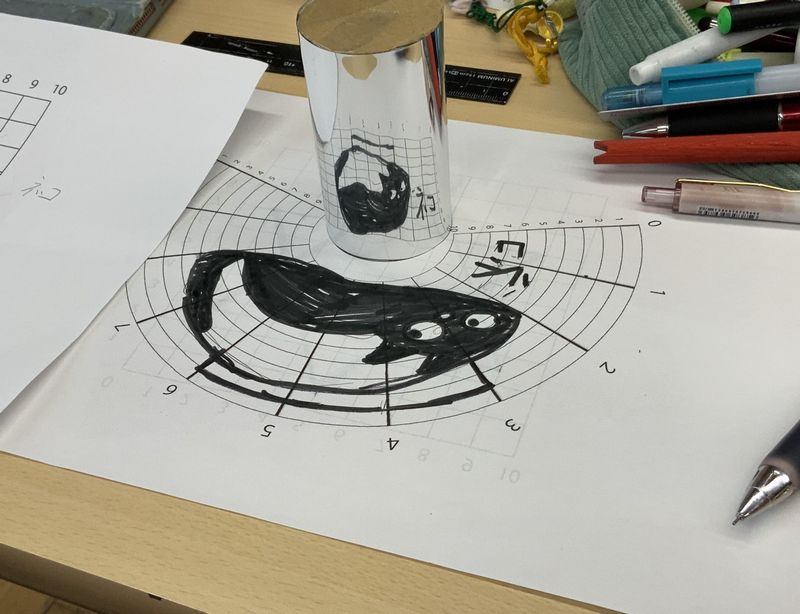
その後、中学生の皆さん自身が円柱鏡、円すい鏡を使ってトリックアート、アナモルフォーシスを作りました。日本では江戸時代にもあって刀の鞘(さや)を鏡にして作っていたので「鞘絵(さやえ)」と呼ばれていたそうです。普通の直交座標(タテヨコの目盛りだと思ってください)に描きたい絵を描いて、それを円柱鏡用の目盛りが入った台紙に書き写します。台紙の中央部に円柱鏡を置くと、普通の絵が再現されて確認することができます。
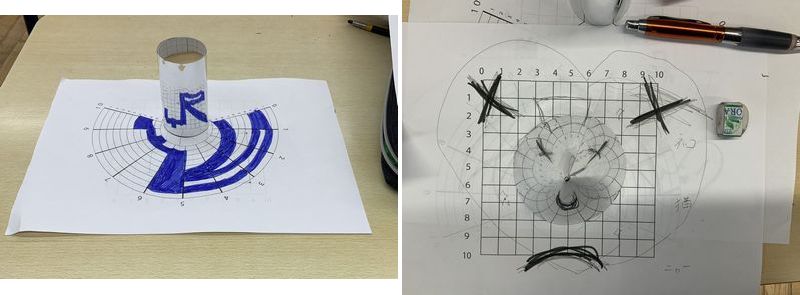
円すい鏡のデザインは、元絵の内側が台紙では外側に描くので円柱鏡より格段に難しいです。人の形を描くとすると、足を外側に描いて顔のパーツを円すいのすぐそばに描くことになります。このイメージが湧きにくいのですが、参加された3年生小寺衣織さんは上手にデザインを作成し、あっという間に原理を把握されたようでした。
最後に、倉橋さんから、映像でサッカーを観戦しているときに芝生に看板が立っているように見えるのも錯視の1種でおもしろいよと紹介してくださいました。
2024年度も、錯視・トリックアートの学びプロジェクトを実施していきます。ぜひ皆さんのご参加をお待ちしております。
(数学科 園田毅)