2023年9月、2学期最初の1年生向けの特別授業で、「地球を測ろう！」というテーマで地球1周（子午線）の距離を測定、計算によって求めました。（関連単元：比、比例、円、おうぎ形）
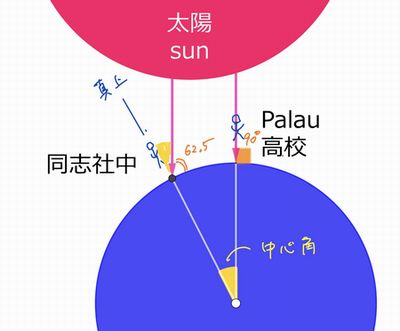
紀元前のエジプトで、数学者エラトステネス（紀元前276頃－紀元前195頃）は2都市間の距離と緯度の差から子午線1週の距離を求めました。緯度の差は、シエネとアレクサンドリア2都市間の太陽高度を測ることで求めました。緯度の差が2都市間を円弧とするおうぎ形の中心角になります。
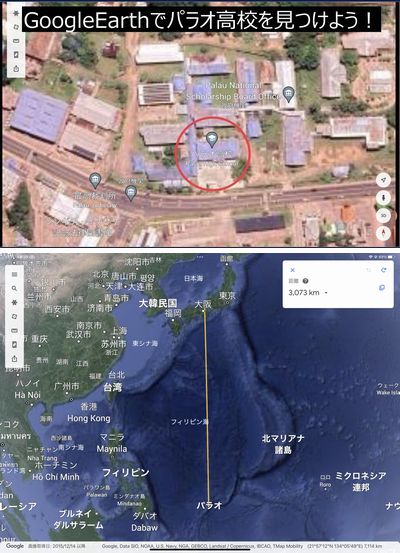今回は、本校とパラオ共和国のパラオ高校を2地点として子午線1周の距離を計算するという授業をしました。元立命館宇治・立命館守山中高で働いておられた長谷川幹（つよし）さんが、海外シニア協力隊員としてパラオに算数・数学を教えに行っておられて、かつ9月３－５日あたりがパラオで真上に太陽が来るということで実現しました。
※なぜ9月に真上に太陽が来るのか不思議に思われた方は、パラオの位置を調べて考えてみてください。
どちらもほぼ東経135°でしたので2地点はほぼ南北に位置しています。過去、比例の単元で学校内の南北道路を歩くことで距離を測り、伊能忠敬的に計算する実践をやったことがあり、今回はエラトステネスバージョンです。
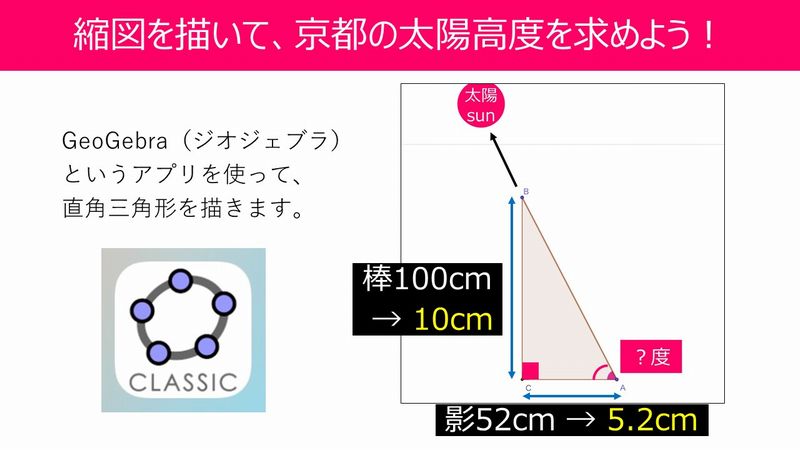
距離はGoogleEarthで求め（3073km）、京都の太陽高度は私が外で１ｍの棒の影の長さを測り（50cm強）、数学アプリGeoGebraでその縮図となる直角三角形を描いて約62.5°と求めました。
この2つのデータから地球1周の距離を計算しました。有効数字の設定（小数点以下の数値をどこまで採用するか）の違いにより、3万9900km ～ 4万300kmが算出されました。エラトステネスは4万6000kmと計算しましたので、かなり正確な数値が出ました。
今回の実験は教員が行い、中学生の皆さんは教室の中で映像を見てもらい、アプリを使って2地点間の距離と太陽高度を求めました。パラオからの映像では、屋外照明塔のポールの影が全くなくなり、円形の電球シェイドの影が真下にまん丸に映っていて、皆さん驚いておられました。
エラトステネスの偉業を現代の科学技術（アプリ）を用いて追体験した学びでした。
（数学科 園田）
