●互除法(ごじょほう)で最大公約数(GCD)を求めるプログラム(Scratch)
中学1年生、田中一奨さんが作ったプログラムをご紹介します。
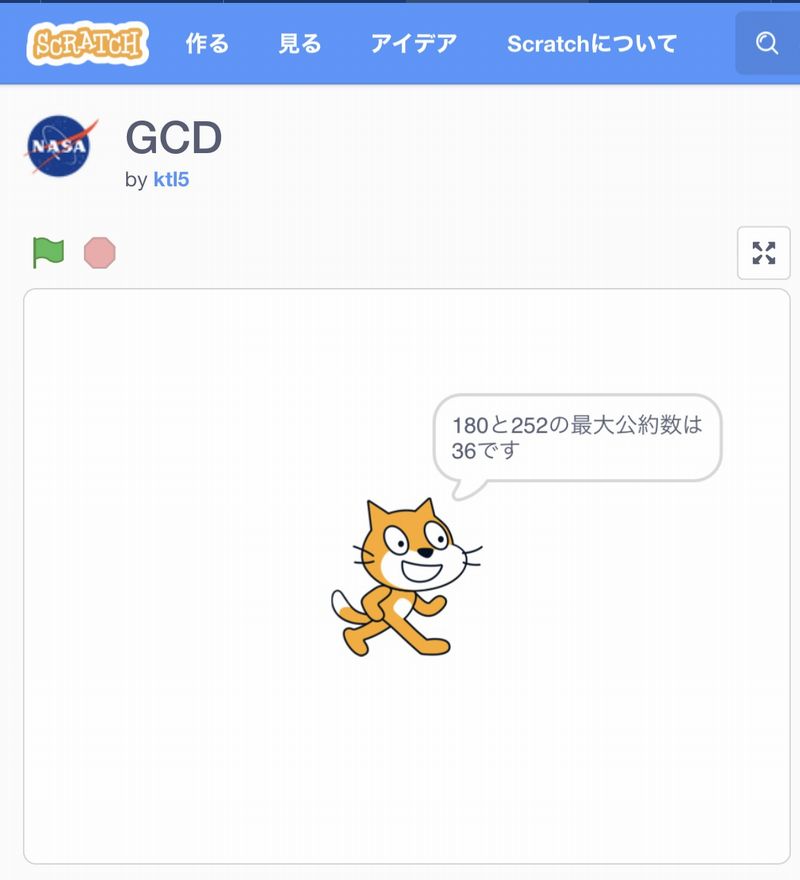
2つの自然数を入力すると、2数の最大公約数(GCD Greatest Common Devisor)が示されるというものです。画面左側の猫の絵の上にあるフラッグをクリック(タップ)すると、プログラムがスタートします。まずは、試してみてください。
https://scratch.mit.edu/projects/747106800
2数の最大公約数(GCD _ Greatest Common Devisor)を求める方法と言えば、まず素因数分解を思いつく方が多いのではないでしょうか。
実はもう一つ、「互除法」によって最大公約数を求めることもできます。私は、図形(2数をタテ・ヨコとする長方形)で原理を説明して、計算方法を導入しました。その際、私たち人間は素因数分解を使って最大公約数を探すが、コンピュータは互除法で求めていることを話すと、何人もの生徒さんがプログラムを作ってきてくれました。次の授業で紹介して、皆さんに体験してもらいました。数学、プログラミングへの興味・関心を深めてもらえるとうれしいです。
180と252の最大公約数が36であることは、次の計算で求めることができます。

180と252の最大公約数(GCD)を互除法によって求める計算は次のような手順になります。
①252を180で割って、1余り72が出ます。
②180を①の余り72で割って、2余り36が出ます。
③72を②の余る36で割ると、2でちょうど割り切れます。
④計算が割り切れたときの「割る数 36」が、180と252の最大公約数(GCD)となります。
これが互除法です。どのような2数でも割り切れるまで計算すれば、必ず最大公約数(GCD)を求めることができます。なぜこのような計算で最大公約数(GCD)を求められるのかを、次回、ご紹介していきます。
(数学科 園田毅)



