中学1年生の学習は「正負の数」という単元から始まります。中学校で初めて学ぶ負の数を理解するために、現実に使われている温度や水位、時差、ゲーム差、ゴルフのスコアなどを紹介しつつ授業を進めています。
負の数を子どもたちが「見る」機会は意外とないものです。例えば、重力や浮力の学習であれば、子どもたちはモノが落ちること、人は海で浮かぶことをすでに経験しているでしょう。経験済みの状況で、重力や浮力のしくみや構造、理由を考えていけるのですが、負の数はそれが難しいのです。
本校では、トランプを使って負の数の存在と演算を学ぶ授業があります。単元前半の学習のポイントは「負の数を『引く』」という概念を身につけることです。理解のポイントは-
●「キャンセル」(打消し)の概念の獲得
例えば、数直線による負の数の導入を考えてみましょう。数直線上の2数の差を見て、 
(+2)-(-5)=+7
となるわけですが、数直線のみで正負の数の加減を理解するためには、
①数直線がそもそも現実の量の集合を抽象化したものであること
(知っている方は銭形平次の投げ銭のひもを思い浮かべてほしいです。)
②さらには、「キャンセル」(打消し)の概念を理解できていることが、負の数を含んだ計算の理解の前提となっています。2数をたせば必ず増えるという「常識」がひっくり返り、「消えたり、減ったり」するという新しい「常識」を身につける必要があります。簡単に示せば、以下のようになります。
(○が+1、●が-1のイメージです。)
ⅰ)0は何もないことを表しているのではない。
ⅱ)さらに、他の数にも同様のことが言えて、2は何かが2個あることだけを表しているのではない。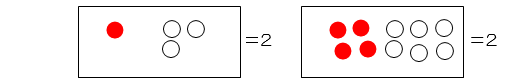
キャンセルの概念を理解して初めて、数直線の負の部分が0から左に「-1、-2、-3、-4・・・」となることも納得できます。負の数を理解するには、正の数だけの世界にはなかったキャンセル概念を獲得することが必要です。
●「負の数を『引く』」ことと、「正の数を『足す』」ことが同値であることを「体験」する 数直線で負の数の減法のしくみを理解するためには、2数の差を見ることになります。
(+3)-(-5)=+8
となり、当然、(+3)+(+5)も「+8」になるので、同じことなのだと説明はできるのですが、負の数を初めて学んだ中学生としては、理屈はわかるが、実感がほしいところです。キャンセルの概念モデルを使うと、以下のように考えることができます。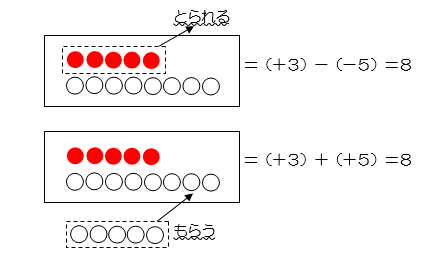
●マイナスの数量をトランプゲームで実感
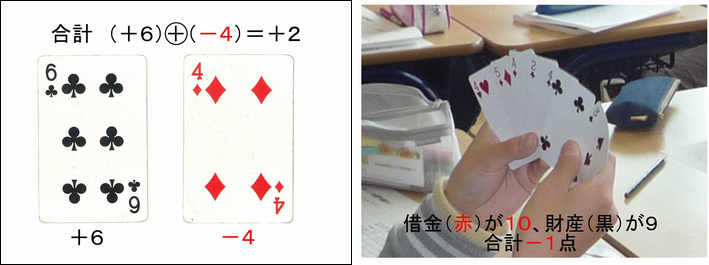
4~5人1班で、トランプゲームをおこないました。遠山啓(数学者 1909-1979)が作り出して以来「赤と黒」という名前で呼ばれているゲームです。トランプのスートが黒の札(クラブ、スペード)を「プラス」、赤の札(ハート、ダイヤ)を「マイナス」として、その(プラスの)得点の多さを競います。
このゲームの中に「赤の手札を取られると自分の持ち点が増える」場面があります。この場面こそが、まさに「負の数を『引く』」演算に対応する操作なのです。
数学を教えるとき、その全貌を知っているゆえに、まず抽象的に定義を教えてしまうことがあります。また教科書がそのようになっている場合も多々あります。
数直線のみ(式の操作)による説明は、式の上ではそうなるということであり、すでにわかっている側の理解です。「マイナスの数をひくとプラスになる」ことが子どもたちにとって、「納得」に至るためには、「現実の世界」、「現実の体験」がくっつけることが大切だと考えています。
●参考文献
「楽しくわかる中学数学の授業 1数と量」 銀林浩監修 あゆみ出版
「ゲームで遊ぼう算数・数学」 小沢健一編 国土社
「数学ワンダーランド1 アリスと悟空の数学旅行(正の数・負の数)」榊忠男 国土社
(数学科 園田毅)



