祝卒業
中学3 年生が作ったシェルピンスキー四面体が完成しました!
同志社中学校数学科

2019年度の中学3年生は、ピタゴラスの定理の応用で、牛乳パックで作った正四面体と正八面体の体積を計算しました。1Lの牛乳パックを約半分(高さ12cm)に切ったパーツで、一辺14cmの正四面体1つ、パーツ2つで正八面体を1つ作りました。これらの体積を、ピタゴラスの定理を使って計算すると意外な結果が出ます。興味のある方はぜひ体積を計算してみてください。その後、1人1つ作った正四面体を合わせてシェルピンスキー四面体を製作していきました。
数学1 教室に完成した16 段のシェルピンスキー四面体です。中学生は授業中にグループで4 個、2 段まで作って休校になりましたので、最後の組み立ては数学科教員4 名(田畑、澤田、樫本、園田)で3 月17 日に行いました。
正四面体1つの高さは、14√6/3cm(約11.4cm)、これが256個、16段に重なって、180cmを超える(11.4×16=182.4)シェルピンスキー四面体ができあがりました。数学教室の真ん中に完成させました。
3年生の皆さん、ご卒業おめでとうございます!!

上の写真は、64個による大きなシェルピンスキーの山が3つできたところです。4個の山(2段の正四面体)をシェルピンスキー四面体1ユニットとすると、牛乳パック4個の容積と中空部分の体積は同じです。しかし、4ユニット(16個4段)、16ユニット(64個8段)、64ユニット(256個16段)になるにつれて、牛乳パックが占める容積は完成されたシェルピンスキー四面体の4分の1、8分の1、16分の1になってしまいます。
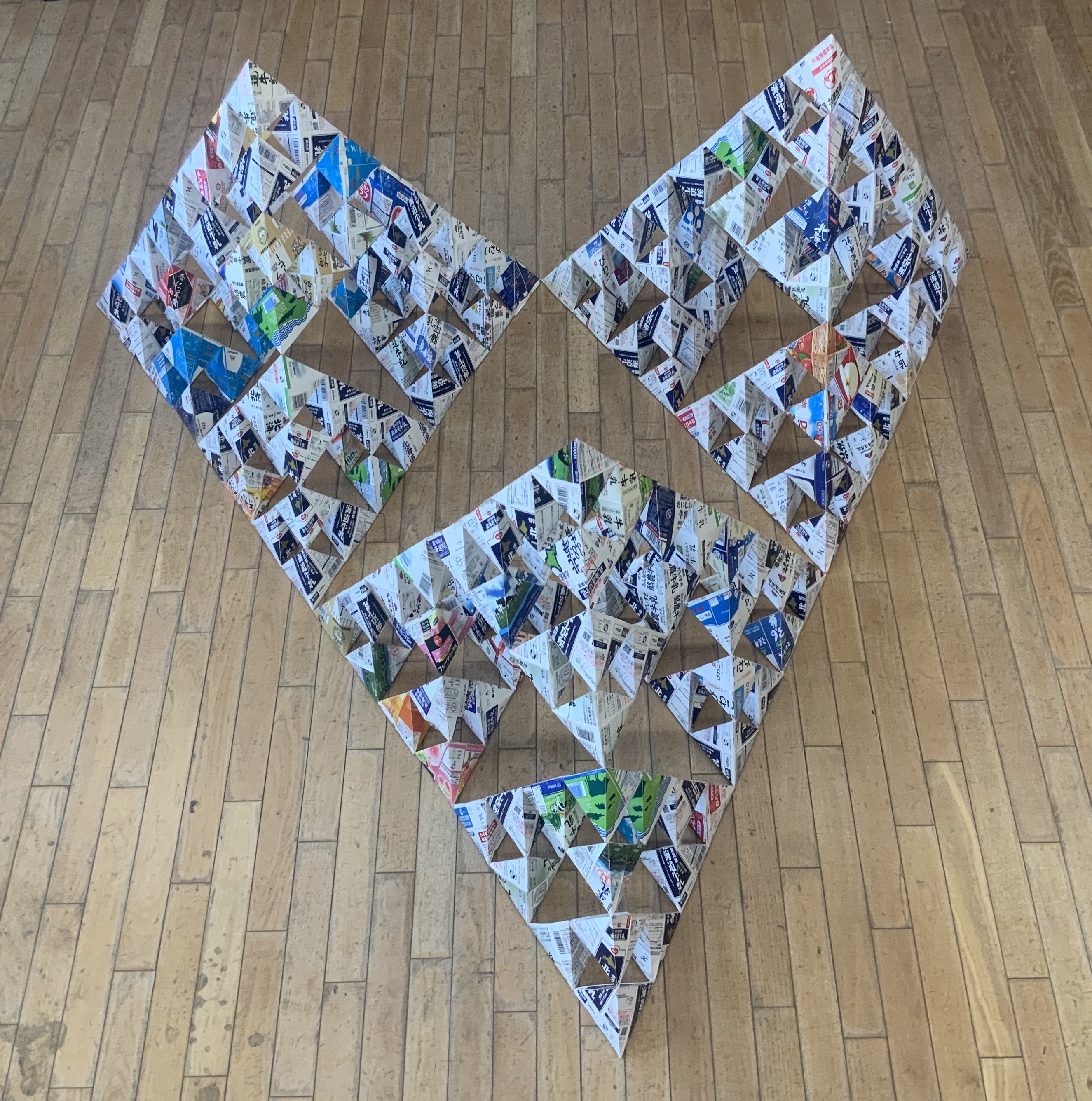
ちなみに、数学1教室の名前は「ピタゴラス」です。今回の立体(正四面体、正八面体)の体積計算に必要なあのピタゴラスの定理を発見した人だと言われています。
興味を持ってくださった方は、ぜひシェルピンスキー四面体や「フラクタル図形」、ピタゴラスの定理について調べてみてください。
卒業生の皆さんの今後のご活躍を心より願っております。
(文責 園田毅)



