本日9月29日を929と3ケタの数で表すと、929は素数です。西暦を含めた20160929は17と69761で割り切れるので、素数ではありません。皆さんも計算してみてください。
１＋２²＋３²＋…＋○²
と続く、自然数の２乗の合計はいくつになるのか考えてみましょう。
実は公式があります。１から○までの自然数の２乗の合計は次のような形にまとまります。高校生、大人の方は、○の部分をｋやｎで学習した記憶があるのではないでしょうか。
１²＋２²＋３²＋…＋○²
＝１＋４＋９＋…＋○²
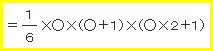
この公式を具体的に立方体の個数として表したのが、この模型です。（写真1）白の立方体が1個、黄が4個、水色が9個、青が16個、橙が25個となっています。この模型は、５² までの合計のモデルにしたので、➄という数字に注目してください。
この模型を３セット合体すると、写真2のようになります。
がんばって、６セット合体してみてください。写真3のような直方体になります。
このとき、全ての立方体の個数を直方体の体積として考えることができますね。
➄を○に直すと、公式ができますね。
“What is the sum of natural numbers squared?”
Let’s talk about the sum of natural numbers squared.
There is a formula.
１²＋２²＋３²＋…＋○²
＝１＋４＋９＋…＋○²
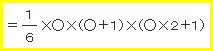
This model is specifically indicating the formula as numbers of small cubes.
There are 1 piece of white cube, 4 pieces of yellow, 9 pieces of light blue, 16 pieces of blue and 25 pieces of orange.
Please check the number 5 in case of n=5 on this model.
First, we combine 3 sets of this model into 1 solid, as we can see in figure2.
Second, we combine 6 sets of this model into 1, so we can see a rectangular parallelepiped in figure3.
So we can see the length of the rectangular parallelepiped in figure3.
When we change 5 into n, we can get the formula!
