今日2月11日を3ケタの数で表すと、211は素数です。西暦を含めた20200211は、 19×29×61×60131と素因数分解できるので素数ではありません。
数学エリア3階の本棚の上に、「フィボナッチ数」が書かれた板を設置してあります。フィボナッチ数(数列)は、
1、1、2、3、5、8、13、21、34、55 ・・・
と数が続いていきます。直前の2つの項をたすと、次の項になるというしくみです。
フィボナッチ(1170頃ー1250頃)は、彼の著書「算盤の書」(1202)の中で「ウサギの問題」としてこの数たちを紹介しました。次のような内容です。
<ウサギのつがい(組)の増え方>
(1)1組のウサギは産まれて1ヶ月で大人になり、2ヶ月後から1組のウサギを産む。
(2)ウサギは死なない。
スタートは赤ちゃんウサギ1組です。1ヶ月後は大人ウサギ1組になり、2ヶ月後は大人ウサギ1組と赤ちゃんウサギ1組で計2組、3ヶ月後は大人ウサギ2組と赤ちゃんウサギ1組で計3組、4ヶ月後は大人ウサギ3組と赤ちゃんウサギ2組で計5組…というふうに増えていきます。
また、フィボナッチ数は自然の中に実際に存在していることで有名です。ひまわりや松ぼっくり、パイナップルの螺旋の数、多くの花びらの枚数がフィボナッチ数になっています。
さらに、フィボナッチ数にはおもしろい性質があります。1つの数をその手前の数で割ると、 だんだん「黄金比=1.618 ・・・ 」と表される数に近づいていくのです。最初は1/1=1からスタートしますが、3/2=1.5、 5/3=1.666 ・・・ 、 8/5=1.6、 13/8=1.625と進み、あっという間に1.618 ・・・ に近くなっていきます。
フィボナッチ数の魅力をいくつか紹介しました。興味を持ってくださった方はぜひ調べてみてください。
(数学科 園田毅)

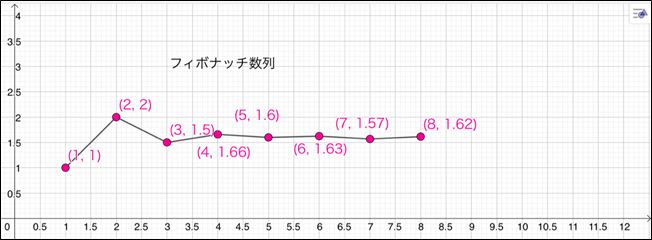
下のグラフは、1つのフィボナッチ数をその手前の数で割ると、だんだん「黄金比=1.618 ・・・ 」と表される数に近づいていく様子をGeoGebraで描いたものです。y座標がだんだん1.618 ・・・ に近づいていきます。
GeoGebraは、幾何、代数、解析を1つに結びつけた動的数学ソフトウェアです。
参考URL: https://sites.google.com/site/geogebrajp/

ジョセフ・ダグニーズ著、ジョン・オブライエン画
「フィボナッチー自然の中にかくれた数を見つけた人」
2010 さえら書房
三浦伸夫著
「フィボナッチ アラビア数学から西洋中世数学へ」
2016 現代数学社

“Fibonacci numbers board”
We put the board with “Fibonacci numbers” written on it on the bookshelf on the third floor in our math area.
Fibonacci numbers (sequence) are below.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ・・・
The previous 2 numbers make the present number. For example,
1+1 = 2、5+8 = 13、21+34 = 55 etc.
Fibonacci introduced these numbers as the problem with rabbits in his book ‘Liber Abaci’ (1202). The contents are as follows.
Way of increasing rabbit pairs
(1) A pair of rabbit become an adult 1 month after their birth and have a pair of babies.
(2) Rabbits never die.
First, there is 1 pair of baby rabbits. They become 1 adult pair 1 month after birth, become 2 pairs including 1 adult pair and 1 baby pair 2 months after, become 3 pairs including 2 adult pairs and 1 baby pair 3 months after, and become 5 pairs including 3 adult pairs and 2 baby pairs 4 months after.
Also, Fibonacci numbers are famous for its presence in nature. The numbers of spiral in a sunflower, a pine corn and a pineapple, and the numbers of many kinds of flower petals are Fibonacci numbers.
Besides, there are interesting characteristics in Fibonacci numbers. The answer of the value what a Fibonacci number divided by the second number
gets close to the golden ratio. 3/2 = 1.5, 5/3 = 1.666 ・・・ ,
8/5 = 1.6, 13/8 = 1.625, it is getting close to 1.618・・・ in this way.
We introduced the fascination of Fibonacci numbers. Let’s research them if you take an interest in them.
by Tsuyoshi Sonoda (Math Dept.)




