本日1月31日を131と3ケタの数で表すと、131は素数です。西暦を含めた20190131は13×281×5527と素因数分解できるので、素数ではありません。
茶色のチョコとホワイトチョコのブロックが2つずつ、合わせて4つあると考えてください。
チョコを見ないままで4つを下の図のように並べると、同じ色が隣りあうときと、茶色と白が
交互に並ぶときがありますね。
それぞれの場合の確率はどうなると思いますか。同じでしょうか、それとも違うでしょうか。
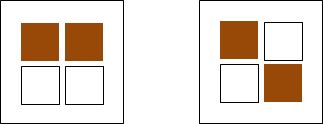
正解は、「2:1で同じ色が隣りあうときが多い」です。確率はどちらも同じだと思った人が多いのではないでしょうか。
直線に並べた場合で考えるのがコツです。6通りの可能性が考えられます。
①茶-茶-白-白 隣りあう
②茶-白-茶-白 繰り返す
③茶-白-白-茶 隣りあう
④白-茶-茶-白 隣りあう
⑤白-茶-白-茶 繰り返す
⑥白-白-茶-茶 隣りあう
となり、隣りあうほうが交互になることより2倍多いのです。
(数学科 園田)

“What is the probability of arranging 2 kinds of chocolate?”
There are 4 pieces of chocolate, 2 pieces are brown and 2 pieces are white.
When those are mixed without looking them, there are 2 cases. One case is that same color chocolate pieces are next to each but the other, other case is that different color chocolates alternate.
What do you think the probability of each case is? Is the probability of each case the same or different?
The answer is that probability of the case that the same color chocolates are next to each other is bigger than the other case.
This is the hint to think the case that the chocolate pieces follow in the line. There are 6 patterns.
(1) Brown – Brown – White – White
(2) Brown – White – Brown – White
(3) Brown – White – White – Brown
(4) White – Brown – Brown – White
(5) White – Brown – White – Brown
(6) White – White – Brown – Brown
So probability of the case that same color chocolates are next to each other is 2 times bigger than the case that different color chocolates alternate.
by Tsuyoshi Sonoda (Math Dept.)




