本日9月19日を919と3ケタの数で表すと、919は素数です。西暦を含めた20180919は、3、11、そして611543という素数で割れるので、素数ではありません。
前回のブログでは、サイクロイドという曲線が急に出てきて、見たことのない式や記号(θ シータ)が入っていて難しく感じられたと思います。今回は、皆さんにサイクロイド曲線をわかりやすくご説明します。
サイクロイドは、一般的に、円が直線の上を転がったとき、円周の上の1点が動く模様を描いた曲線です。自転車のタイヤについているマークが、タイヤが道路を転がるのに合わせて動いていく様子をイメージするとわかりやすいと思います。
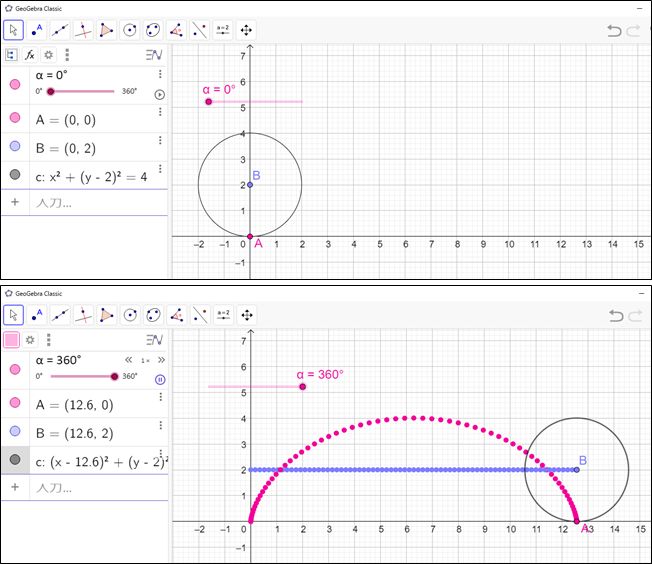
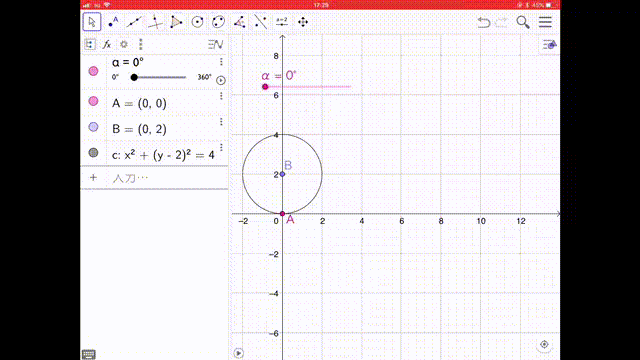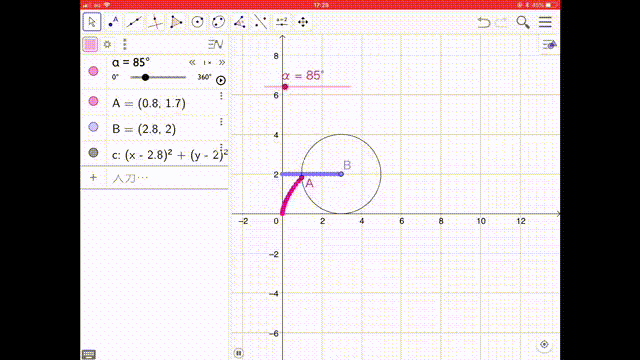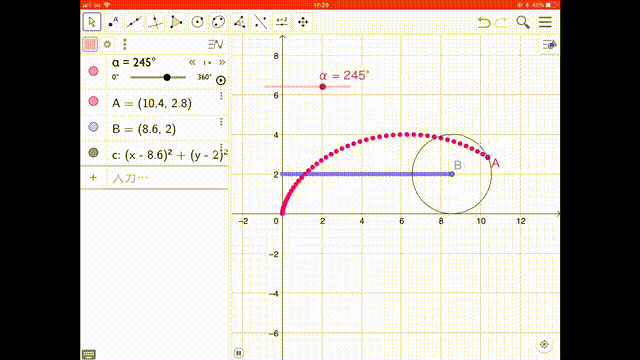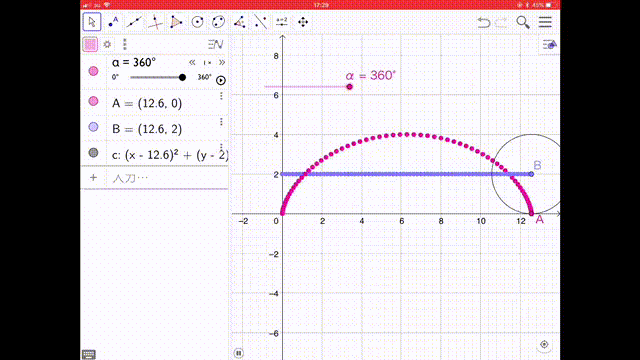
今回は、GeoGebra というグラフソフトで描きました。このグラフでは、動く点(動点 どうてん)は原点からスタートしています。動画で、円が動くとともにサイクロイド曲線ができていく様子を見てください。サイクロイドすべり台は、このグラフの上下をひっくり返したラインの形になっています。
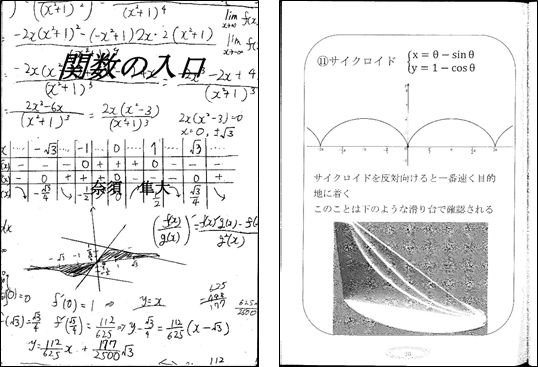
2015年に、中学3年生の奈須隼大さんが自由研究でいろいろな関数をまとめて作成された「関数の入口」という冊子にもサイクロイドが紹介されていました。
サイクロイド曲線は1年生の授業で、10円玉はタイヤ、定規は道路のイメージで10円玉の1ヶ所に鉛筆を当て、定規の上を転がして描いていきます。円もそうなのですが、点がある規則で動くと、きれいな線ができますね。
(数学科 園田)
“Cycloid slide 2”
You may feel that it was difficult to read the last blog and to see the unknown mathematical symbols in the expression of cycloid.
We want to explain how to understand cycloid curve in this blog.
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line generally.
It is easy to understand if you imagine that a mark on a wheel of a bicycle rolls on a road.
We wrote a cycloid using an application called GeoGebra. The moving point of this graph starts from origin. Please check this movie. It will be the graph of cycloid with a circle moving. This cycloid slide is a opposite shape of this graph. In 2015, a 9th grade student Nasu hayato san wrote a book “The Entrance of the Function” in his research work and he introduced a cycloid graph.
In our 7th grade student’s class, they write cycloid graphs using a pencil along one point of a 10-yen coin rolling on the scale. We can see beautiful lines with the point moving according to the rules like a circle.
by Tsuyoshi Sonoda (Math Dept.)



