本日9月7日を907と3ケタの数で表すと、907は素数です。西暦を含めた20180907は、36×19×31×47と素因数分解できるので、素数ではありません。
今回、ご紹介するのは、木製の「サイクロイドすべり台」です。スタートとゴールを同じにした3つのコースにビー玉を同時に転がして実験します。直線、放物線（2次関数）、サイクロイドと呼ばれる曲線の3コースでそのスピードを競います。
結果は・・・サイクロイド曲線のルート(写真で最も手前のライン)を通ったビー玉が最も速くゴールに到達します。ジェットコースターのコースはできるだけスピードが出るようにサイクロイド曲線をもとに設計されていて、サイクロイド曲線は「最速降下曲線」とも呼ばれます。
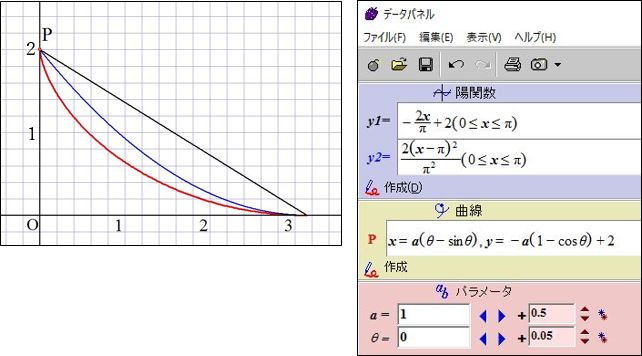
次に、写真で実物とその設計図面（グラフ）を紹介します。GRAPESというソフトで、高さ2、水平距離3.14（円周率）という設定でグラフを描きました。実際の高さは50cmです。サイクロイド曲線の式は表現が難しくて、媒介変数θ（シータ）というものを使って、この図の場合は、
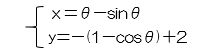
というふうに表されます。
このすべり台はリスーピアはじめ各地の科学館にありますが、本校には現在高校生のご家族の方が2015年に作ってくださった模型もあります。
（数学科 園田）
We will introduce our wooden “Cycloid slide”. We can experience this by rolling three marbles at the same time on the three courses that have same start point and goal point. We research which marble rolls most quickly on the courses of a linear function, a parabola and a cycloid.
The result is that the marble on a cycloid line reaches to the goal first. Courses of roller coasters are designed based on cycloid curve so that those run as fast as possible and a cycloid curve is called “a brachistochrone curve”.
Next, we will introduce the real thing and its blueprint (graph). We draw graphs where the height is 2 and the width is 3.14 (π). Real height is 50 centimeters. It is difficult to express cycloid curves, so we express
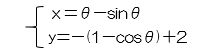
using parameter θ.
There are “Cycloid slides” exhibited in many science museums of Japan. We also have another model our student’s grandfather made in 2015.
by Tsuyoshi Sonoda (Math Dept.)
