本日3月7日を307と3ケタの数で表すと、307は素数です。西暦を含めた20180307は3×7×7×107×1283と素因数分解できるので、素数ではありません。（次回は4月中旬に発信します。）
今回は、夏の自由研究で、昨年に引き続き、Rimse理数教育研究所主催「算数・数学の自由研究」作品全国コンクールで敢闘賞を受賞された池田はるなさん（3年生）の作品を紹介します。
（主催者HP http://www.rimse.or.jp/research/past/winner5th.html ）
テーマは「おじいさんはおむすびに追いつけたのか！？ おむすびころりん徹底検証！！」 です。
日本のおとぎ話として有名な「おむすびころりん」では、おじいさんはおばあさんが作ってくれたおむすびを落としてしまい、おむすびは山の斜面を転がります。おじいさんはすぐ追いかけましたが追いつけずに、おむすびは木の根元にあった穴に落ちてしまったという設定でお話は展開していきます。池田さんのレポートは、高校の物理で学ぶ運動法則ｘ＝ｖ0ｔ＋
ａｔ2（ｘ：移動距離、ｖ0：初速度、ｔ：時間、ａ：加速度）を使って、このお話を実際に実験、検証しています。傾斜の角度、おむすびの形・重さ、おじいさんの走る速さを変えて実験し、それぞれの影響を分析しました。イラストや実験データ・グラフが多用されていて、読ませるレポートに仕上がっています。
彼女は1年次に「コップの容積をパッ！と求めるには!?」というテーマで、2年次には「見た目の形と距離の関係 ～地面のタイルまでの距離が遠くなると，タイルが平たく見えるのはなぜだろう？？～」というテーマで数学の自由研究にとりくみました。どれもたいへんわかりやすいレポートです。
池田はるなさんの作品はすべて立志館2階数学MS1に展示してあります。
（数学科 園田）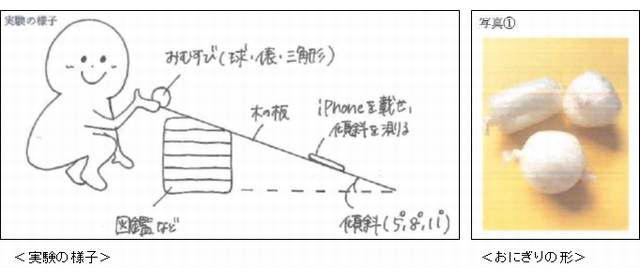
“Thorough Research of ’Omusubi Kororin’”
This is the title of a student’s research during the last summer vacation part1.
We will introduce our student’s research work. Ikeda Haruna san (9th grade) got a prize in the competition by “Rimse” Research Institute of Mathematics and Science Education for two years in a row.
The title of her research is “Thorough Research of ’Omusubi Kororin’ – did an old man catch up with an Omusubi?”
In an old Japanese story called ‘Omusubi kororin’, an old man dropped an omusubi that an old woman made for him and it was rolling down the slope of the mountain. He ran and tried to catch up with the omusubi, but he could not and it fell in a hole near the foot of a tree and the story continued. Ikeda san used the law of motion ‘ｘ＝ｖ0ｔ＋ａｔ2（ｘ : movement distance, ｖ0 : initial velocity, ｔ : time, ａ : accelration）’ and researched this story. She changed conditions of the degree of the slope, the shape and weight of the omusubi and the velocity of the old man running and tested it. And she verified the influence of those conditions. Her report used many illustrations and graphs, it was a very rewarding work.
She made projects, ‘How to get the cubic contents of glasses’ in the 7th grade and ‘Relativity of the shape of appearance and distance – why is that the more further away the tile on the ground is, the more flat it seems to become?’ in the 8th grade. Both research contents were very clear.
All of her research projects are exhibited on the second floor in our math space.
by Tsuyoshi Sonoda (Math Dept.)
Click Here for report(PDF)
