今日9月7日を907と3ケタの数で表すと、907は素数です。西暦を含めた20170907は823と24509という２つの素数で割り切れるので、素数ではありません。3ケタ以上の素数はプログラムを用いないとすぐには発見できませんね。
展開・因数分解パズルの第3弾です。
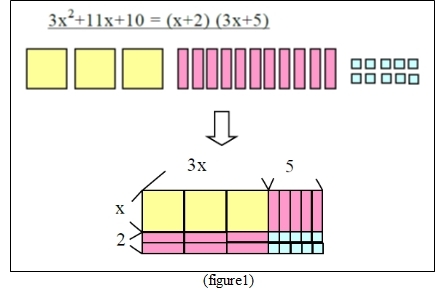前回のお話で、このパズルが展開・因数分解をイメージしているものであることはおわかりいただけたと思います。
そして、このパズルをより抽象的、象徴的に表したものが面積図や直積表と呼んでいるものになります。
(figure2、figure3)
皆さん、今までは式の中の数値が「＋」（プラス）であることを前提にお話をすすめてきましたが、今回は、項がに「－」（マイナス）があるとき（係数や定数項が負の場合）について考えてみます。実は、今までと同じように直積表で解決することができます。「＋」（プラス）のときと同じように長さとして考えればよいのです。
x2＋5x－14 の因数分解について、実際に解きながら考えてみましょう。
まず、x2 と －14 を直積表の左上と右下に記入します。－14 は負の項なので、直積表では赤い枠で表現しています。
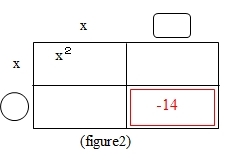かけて－14になる数を
と
にあてはめて、右上と左下の合計が＋5xになる組を探します。
（＋1, －14）、（－1, ＋14）、（＋2, －7）、（－2, ＋7）の４組をあてはめて、（－2, ＋7）の組み合わせが正解とわかります。
展開・因数分解が解けることはひらめきや才能と関連があると思っている方もいらっしゃるかもしれません。そうではありません。今の操作を下図に示しました。この問題は最大4回の試行錯誤で必ず正解が出るのです。因数分解パズルで、試行錯誤して正解を見つけることを楽しんでください。(数学科 園田)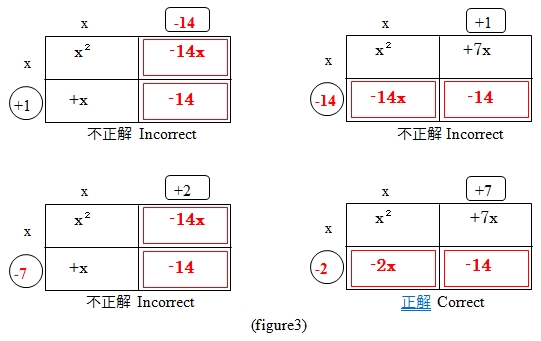
“Expansion & Factorization puzzle 3”
We can use negative numbers as a 2nd step. x2+5x-14 = (x-2) (x+7)
Write “direct product table”, “x2“ and “-14” in the frame, “x” and “x” left and above the upper left box, the same as in example 1.
With trial and error, then we can solve it.
Think of the numbers of and . The numbers times each other is -14. (+1, -14),(-1, +14), (+2,-7) and (-2, +7) groups are considered. At first, I write +1 and -14 in the blank. Then the amount of term of x is -13x. So I know that +1 and -14 are incorrect.
After several trial and errors, I write -2 and +7. The amount of term of x is +5x. So I know -2 and +7 are correct.
I think that an ability of solving expansion & factorization is not connected with talent of math. We can solve this problem by trial and error less than four times.
Please try and enjoy this puzzle!
