正12角形の中心から頂点に引いた線の長さを「ｒ」cmとすると、正12角形の面積は「３ｒ2」cm2 になります。算数で計算できるものとして、中学入試で出題されることがあります。
先日、数学博物館を気に入ってくださっている中学1年生の数井沙和さんが、これを可視化して説明する展示物を作ってきてくださいました！
夏休み前に、展示を作ることにチャレンジしてみてと私が話したことを覚えていてくださって、夏休み以降作っておられたのでした。
数井さんが制作された正12角形は発泡スチロールに紙を貼り、着色されています。正三角形(青)と底角15°の二等辺三角形(黄)を組み替えると、長さ「r」の正方形3つになります。４枚の連続写真をご覧ください。
計算で求めるときは、中心Oから各頂点へ引いた線で、分割した二等辺三角形OAB（頂角30°、底角75°）の面積を求めて、それを12倍して求めます。
等辺の長さを「ｒ」cmとします。
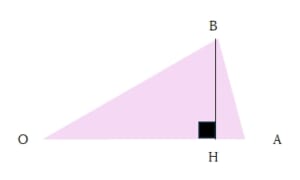
右図のように二等辺三角形を配置して、頂点Bから辺OAに垂線を引くと、三角形BOHは∠BOH＝30°、∠HOB＝60°、∠BOH＝90°の直角三角形が見つかります。
ここから、三角形OABは、底辺OA＝ｒ、高さBH＝ 1 2 ｒとわかり、その面積は、
ｒ× 1 2 ｒ× 1 2 ＝ 1 4 ｒ2
したがって、正12角形の面積は、
1 4 ｒ2 ×12 ＝ 3ｒ2
となります。
数学博物館に展示します。
ありがとうございました！
（数学科 園田毅）
