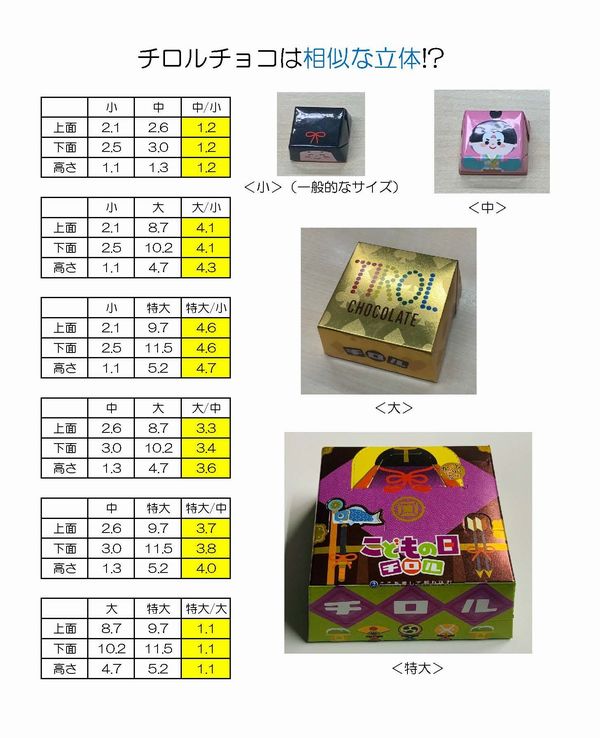
チロルチョコはだいたい相似！？

　毎年、こどもの日に向けてビッグサイズのチロルチョコ「こどもの日チロル」が発売されています。チロルチョコは「正四角すい台」という形をしています。今回、大小のサイズを調べると4種類あることに気づきました。上下面の正方形の1辺と高さを測ってみました。厳密には相似でないですが、だいたい相似でいいかなという寸法でした。ピタゴラスの定理があれば、チョコの高さでなく母線（上下面の正方形の頂点を結ぶ線）の長さからでも体積を求められるのですが、今回、全学年対象の懸賞クイズとして出題したので、高さを測りました。

　「相似」の単元・用語は、中学校の学習内容となっていますが、算数でも「拡大・縮小」という表現で扱われたり、実生活でもコピーや地図など目にする場面が多い教材の一つです。

　中学校の学習では、三角形の相似条件を学習します。①3組の辺の比がすべて等しい,、②2組の辺の比とその間の角がそれぞれ等しい、③2組の角がそれぞれ等しい、というものです。三角形の合同条件と同様、相似条件も3つあります。しかし、四角形以上の多角形のそれは原則2通りになります。（詳しくは、別稿でご紹介します）また、今回のように立体の相似を考えた場合、相似条件はより複雑になっていきます。日本の中高で学習する合同や相似は三角形をメインに学習しますが、最も頂点と辺の数が少ない三角形は特別な図形であり、四角形以上の合同条件や相似条件は三角形の場合を知っていたらすぐわかるものではないです。

　上記のような理由で、相似な図形（多角形）についてより大事なことはその定義です。

　コピー機による通常の拡大（縮小）は、元原稿の角の大きさはそのままで、対応する全ての辺を同じ倍率で拡大（縮小）しているわけです。

　最後は、あたりまえの結論になりましたが、興味を持たれた方は、四角形以上の多角形の合同条件、相似条件についても考えてみてくださるとうれしいです。

（数学科　園田毅）