明日7月1日を701と3ケタの数で表すと、701は素数です。西暦を含めた20170701は3と23と401という3つの素数で割り切れるので、素数ではありません。（明日は土曜日のため今回は前日6/30に発信しました。）次回の発信は9月7日（木）を予定しています。
前回、皆さんに直積表を利用して因数分解を理解するパズルを紹介しましたね。今回はその第2弾です。
このパズルの3種類の板は、
黄 ：一辺xの正方形、面積x2
ピンク：一辺がxと1の長方形、面積x
緑 ：一辺1の正方形、面積1
です。
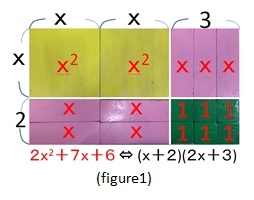
したがって、右の図で、板の種類ごとに面積を表せば、2x2＋7x＋6となりますし、大きな1つの長方形の面積と考えると、(x＋2)(2x＋3)となり、2通りの表現で面積を示すことができますね。
これが展開と因数分解の正体です。また、このパズルを簡単に表した(抽象化した)のが直積表です。たすきがけよりも展開・因数分解のしくみが可視化されていますよね。
（数学科 園田）
“Expansion & Factorization puzzle 2”
The last time, I showed “Expansion & Factorization puzzle”. This time, I will explain the structure of expansion & factorization using this puzzle.
Look at the puzzle in “figure1”. “x2” is an area of a square of a side x, “x” is an area of a rectangle with each side of x and 1. “1” is a squares of a side 1. We can say the total area of those pieces is “2x2＋7x＋6” and can also say “(x+2)(2x+3)”.
This is the true colors of Expansion & Factorization. And “a direct product table” is a model of this puzzle. This model visualizes the structure more clearly than “tasuki – gake”.
