今日2月27日を227と3ケタの数で表すと、227は素数です。西暦を含めた20170227は、3×7×11×87317と素因数分解できるので素数ではありません。
今日2月27日を227と3ケタの数で表すと、227は素数です。西暦を含めた20170227は、3×7×11×87317と素因数分解できるので素数ではありません。
４つの４から四則演算で１つの数を作る遊びがあります。（英語では Four fours） 例えば、２を作るときは、４×４÷（４＋４）＝２ となります。 今回は、次の４つの数から１０を作ることにチャレンジしてください。
（１）１、９、１、９を使って、１０を作ってください。
（２）３、４、７、８を使って、１０を作ってください。
答えを以下に示します。
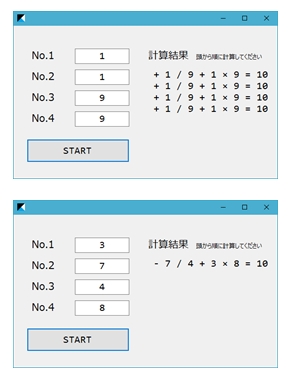
（１）(１÷９＋１)×９＝１０
（２）(３－７÷４)×８＝１０
すでに何人かの生徒たちが正解を持ってきてくれています。この問題は、試行錯誤の中で答えが出てきます。また、今回の問題は答えがありますが、選ばれた4つの数からすべての数が計算できるわけではありません。まさに「数学」ですね。公式の暗記で素早く答えを出すのが数学ではありません。ゆっくりじっくり考えてみましょう。
今月の解答者の中に、この問題の答えを計算するプログラムを作ってきた人がいました。現在3年生の青木隆史さんです。私がこのブログで使っている素数判定プログラム「PrimeFactorization」を作ってくれたのも彼です。
今回の計算結果の画面とプログラムコードの一部を紹介しますね。
（数学科 園田）
“Finding the simplest mathematical expression by using four numbers from 1-9 and only common mathematical symbols”
We will talk about math quiz of February “Masu masu hatten koza” exhibited on the wall in Do★Math. Do you know the math puzzle “Four fours”? For example, “Make 2 by using four fours”, the solution is “4×4÷（4＋4）”. We asked our students,
（1）Make 10 by using 1, 9, 1, 9
（2）Make 10 by using 3, 4, 7, 8
The answers are the following.
（1）(1÷9＋1)×9＝10
（2）(3－7÷4)×8＝10
Some students answered to us. To solve the these problems, use trial and error and find answer. Please think hard and use trial and error.
One student made a program code to solve this problem. He is Mr. Aoki Takashi san (9th grade). He also made the program code “PrimeFactorization” to do the factorization in prime numbers that I usually use.
We will introduce the screenshots of the results of his calculations and the code he made in this blog.
