本日10月13日を1013と4ケタの数で表すと、1013は素数です。なんと、西暦を含めた20161013も素数です！
１＋２＋３＋・・・＋１４＋１５ は？
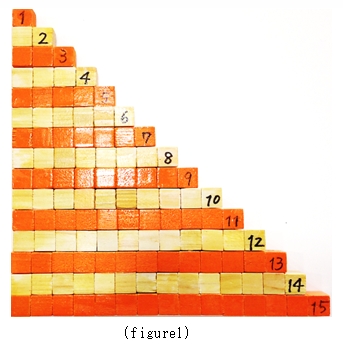
ひとつずつ順に計算していくとたいへんですね。右の階段状の立体(写真1)は、上の式のモデルです。各行の立方体の個数がその行の右端に書いてあります。
だから、階段状の板は、
１＋２＋３＋…＋１３＋１４＋１５（個）
の合計を表しています。
このまま、順にたしていくのはたいへんなので、同じ板を２枚合体させてみましょう。(写真2)
タテが１５ｃｍ、ヨコが１６ｃｍの長方形になりますね。だから、答えは、
１５×１６÷２ ＝ １２０（個）
とな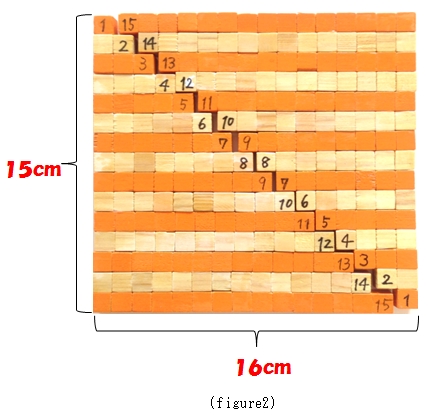
ります！ 確かめてみましょう。
数学者ガウス（ドイツ 1777－1855）は、小学生のとき、１から１００までの数の合計を求める課題を出されたのですが、彼がどのように解いたか、皆さんもうおわかりですね。
１００×（１００＋１）÷２ ＝ ５０５０
“What is the sum of natural numbers?”
１＋２＋３＋・・・＋１４＋１５＝？
It is difficult to calculate one by one.
There is a solid like some stairs. It is a model of the above expression. (figure1)The number on the right side shows the quantum of the small cubes each row.
So this board means the sum of
１＋２＋３＋・・・＋１４＋１５＝？
Now we unite 2 solids into 1 and we can see a rectangle. (figure2)
The vertical length of this rectangle is 15, the horizontal length is 16.
So the answer is
15×16/2=120
There is famous story about the calculation above.
When a mathematician, Gauss (Germany 1777-1855), was an elementary school student, his teacher asked his students to get the sum of natural number from 1 to 100. He soon solved the problem.
You can see his way of solving.
100×(100＋1)/2=5050
