自然数の３乗の和はどうなる？

今日9月19日を919と3ケタの数で表すと、919は素数です。西暦を含めた20170919は1009と19991という２つの素数の積で表されるので、素数ではありません。

１³＋２³＋３³＋・・・＋○³ ＝ ？
この合計はいくつになるでしょうか。

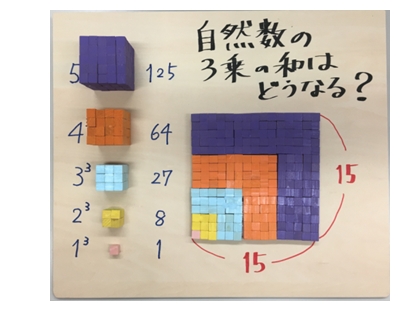
上の模型（fig.1）は、○＝５ の場合を小さな立方体のピースで表したものです。

すべての小さな立方体の合計は、
１³＋２³＋３³＋４³＋５³
＝１＋８＋２７＋６４＋１２５
＝２２５ （個）

となりますね。
この模型は、○＝５ の場合のものなので、５ という数に注目してください。
この模型を平面上に並べると、なんと正方形が出現します！ （fig.2）
だから、合計は

１³＋２³＋３³＋４³＋５³
（１＋２＋３＋４＋５）²
＝１５²
＝２２５（個）

と求めることができますね。
また、高校では以下の公式を学びます。
{○×（○＋１）÷２}²

（数学科 園田）

“What is the sum of natural numbers cubed?”
Let’s talk about the sum of natural numbers cubed.

１³＋２³＋３³＋・・・＋○³ ＝ ？

We will think about above expression.
I show the model in the case of n = 5 shown in fig.1.
The sum of small cubes looks like this.

１³＋２³＋３³＋４³＋５³
＝１＋８＋２７＋６４＋１２５
＝２２５ (pieces)

Next, I put the all pieces of cube on a plane, those make a square. (fig.2)
Then we can find the sum of small cubes like this.

１³＋２³＋３³＋４³＋５³
（１＋２＋３＋４＋５）²
＝１５²
＝２２５ (pieces)

So we also can get the following formula.
{○×（○＋１）÷２}²

by Tsuyoshi Sonoda (Math Dept.)